Libraries and Modules
Two open source libraries were used in our final product. The MCP3008 ADC Python library from Adafruit was used to interface with the MCP3008 ADC over four-pin software SPI. Additionally, he open-source library "pi_ina219" written by Chris Ballard was used to fix conflicting GPIO instantiations by the ADC library and Adafruit.GPIO module.
Several modules were imported in our final product as well. The module "sys" was used to point to the paths where our ADC libraries existed and append them to the in-built Python path. "RPi.GPIO" was imported in order to use the GPIO pins of the Raspberry Pi. The modules "MCP3008" and "Adafruit_MCP3008" worked with the Adafruit ADC library to interface with the MCP3008 ADC chip. "Matplotlib" and "Pyplot" were imported to graph and then save the image of each neuron's action potential. The "Collections" module was used as a high-performance double-sided array. Finally, the standard modules "os" and "math" were used to manipulate operating system functionality and acess basic mathematical functions respectively.
ADC Functionality
As we quickly came to realize, the Raspberry Pi did not come with any analog functionality. As such, we purchased a low-cost 8-channel 10-bit analog to digital converter from Adafruit: the MCP3008.
The MCP3008 has two modes of functionality, hardware SPI and software SPI. Our original intention was to utilize hardware SPI as it is slightly faster and more efficient. However, the hardware SPI pins required by the MCP3008 (SCK, MOSI, MISO, CE0) were already used by the TFT. As such, we implemented a software SPI connection instead. Due to our pin availabilities, the MCP3008 library was modified to use pins 12, 16, 20, and 21 for CLK, CS, MOSI, and MISO respectively. Figure 6 below shows the schematic of our connection between the Raspberry Pi header and MCP3008 chip.
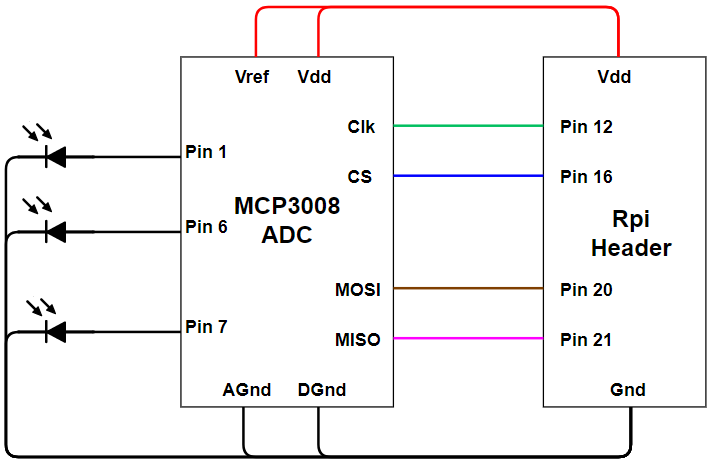 Figure 6: ADC Wiring
Figure 6: ADC Wiring
The ADC was tested by running the "SimpleTest.py" example code provided by the Adafruit team. This code simply iterates through each ADC channel and prints their values every half second on the command terminal. A sample output of this code can be seen in Figure 7 below. Following this, our ADC was up and ready to go!
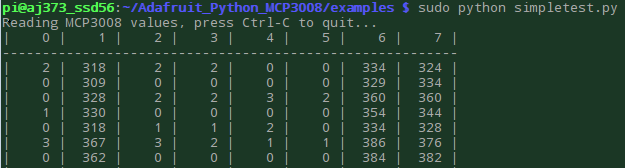 Figure 7: ADC SimpleTest Output
Figure 7: ADC SimpleTest Output
Plotting Graphs
In order to plot the graphs of our neuron action potentials, we used the open-source modules "Collections", MatplotLib", and "Pygame". "Collections" was used to create an array that acted as a rolling FIFO. The FIFO included 50 elements that represented the voltages of a singular neuron at any point in time. At the end of each iteration of code, an element was popped off the left end of the array, and a new value was appended to the start of the array (an artificial FIFO). Three FIFOs were created corresponding to each of the three neurons
We utilized the module "Matplotlib" in order to plot these FIFO data streams on our Raspberry Pi. First, we created a constant range of values from 0 to 50 to resemble time. After iterating through our equations and appending a new element to our FIFOs, we use the 'plot' function to create graphs of each array vs. time. Functions such as 'xlabel' and 'ylabel' as well as keywords such as 'b', 'r', and 'g' were used to modify the graph's axes and colors respectively. Finally, the plot was saved as a .png file into the Raspberry Pi's memory.
Our final step involved using "Pygame" to create our multimedia application on top of the SDL libraries. We initialized a Pygame screen with the correct size of our monitor (960x720 for desktop. 320x240 for TFT) and loaded a Pygame image as our saved Matplotlib figure. Finally, we appended this image to our screen every iteration through our code for a smooth animation experience.
Neural Math
The primary mathematics for a neuron is set by the below equation
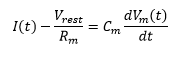 Figure 8: Differential Equation for Leaky Integrate and Fire
Figure 8: Differential Equation for Leaky Integrate and Fire
The neuron fires when the voltage V
m reaches a certain threshold voltage V
thresh . At this point, the neuron spikes. The integrated voltage is directly affected by the stimulating current of the neuron. After a spike occurs, the membrane voltage is set back to resting potential. After the membrane is set to resting potential, its voltage remains constant until the end of the refractory period. As a result, the differential equation can be defined by the time since the end of the refractory period. We can then solve the differential equation to characterize membrane voltage. First, we define the time constant τ as R
m C
m. We define t as the time since the end of the refractory period. Finally, we define I
stim as the current generated by the stimulus. The solution to the differential equation is
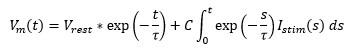 Figure 9: Differential Equation Solution for Leaky Integrate and Fire
Figure 9: Differential Equation Solution for Leaky Integrate and Fire
Implementation in Code
The aforementioned differential equations were implemented in code as follows. We first have several settable parameters. These parameters all effect the final output graph. These settable parameters include tau, the membrane time constant, cap, the membrane capacitance, V thresh , the threshold voltage, and V rest , the resting potential of the neuron. In addition, each of the neurons has a settable excitatory gain and an inhibitory gain. The excitatory gain is multiplied by the stimulus value when the neuron is excited by light and the inhibitory gain is multiplied when it is inhibiting other neurons.
After parameters are set, we run the actual calculations. The same calculations happen in parallel for all neurons. We first set the refractory time, t ref , to 0. This means that the neuron is not currently in the refractory period. If the analog readings of the neuron are less than a threshold, we assume that the stimulus current is automatically leaked. For this reason, the membrane voltage and the integral value are set to the resting potential. If t ref is nonzero, then we are in the refractory period. In this case, we decrement t ref
If the neuron’s value is greater than the threshold, we begin including the stimulus readings into the integral. If t ref is nonzero, we are still in the refractory period, so this value is decremented. In addition, the integral and voltage membrane values are set to the resting potential. The LED used to display neuron spiking is set to output low. Otherwise, if t ref is zero, we are no longer in the refractory period. We increment the value of t refEnd , which is the time since the end of the refractory period. We then add to the integral as in the aforementioned equation. Additionally the stimulus current is changed to include lateral inhibition with the equation below:
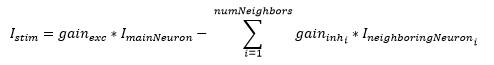 Figure 10: Stimulus for Neuron Adjusted for Lateral Inhibition
Figure 10: Stimulus for Neuron Adjusted for Lateral Inhibition
At each iteration, the integral is updated. In addition, the membrane potentials are updated as in the first equation. If the membrane voltage surpasses the set voltage threshold, a spike is recorded. In this case, t ref is set to 5 to indicate the start of the refractory period. The membrane voltage is set to equal the threshold voltage, and the neuron’s spiking LED is set to output high. If t refEnd is greater than 40, we reset the membrane potential back to the resting potential, as the integration never led to the neuron firing and a spike was not detected. This step is essentially a forced leaking action for the neuron. With that, we have a complete working set of equations to model our neurons!
Box Construction
For constant testing of our optical neurons, we built a box with sliding doors. The sliding doors were used to gradually expose the LEDs to light. With two sliding doors, we were able to choose which neurons were exposed to light as well as cause individual neurons to fire. This allowed for better demonstration of effects such as lateral inhibition.
 Figure 11: Side View of Box
The sides of the box were made with 6 ½ x 3 ¾ x ¾ “ blocks of plywood. The bottom of the box was made with a 4 ½ x 6 ½ x 3/16 “ block of wood. The back of the box was made with a 3 ¾ x 4 ½ ” x 3/16” block of wood. All of these components were attached to each other with screws. In order to make the sliding doors, we attached ½ ” x 6 ½ ” x 1” blocks of wood on top of the sides. We created ¼ ” grooves along the length of these blocks. The sliding doors were two 3 ½ x 3 ¼ x 3/16 “ blocks of wood.
Figure 11: Side View of Box
The sides of the box were made with 6 ½ x 3 ¾ x ¾ “ blocks of plywood. The bottom of the box was made with a 4 ½ x 6 ½ x 3/16 “ block of wood. The back of the box was made with a 3 ¾ x 4 ½ ” x 3/16” block of wood. All of these components were attached to each other with screws. In order to make the sliding doors, we attached ½ ” x 6 ½ ” x 1” blocks of wood on top of the sides. We created ¼ ” grooves along the length of these blocks. The sliding doors were two 3 ½ x 3 ¼ x 3/16 “ blocks of wood.
 Figure 12: Top View of Box
These blocks of wood slide into the grooves on the top of the box to block out light from a hanging lamp. These blocks were designed to block out light from two neurons at a time. We controlled the space between the sliding doors to show how exposure to light affects the neurons. We created a hole in the box to pass the piCobbler ribbon cable through, and attached the raspberry Pi
to the outside of the box using Velcro. We also drilled holes for 3 LEDs to be seen on the outside of the box. These LEDs were used to identify spiking of the left, right, and center neurons. The side view of our box can be seen in figure 11 to the right. Figure 12 shows the top view of the box with the sliding doors.
Figure 12: Top View of Box
These blocks of wood slide into the grooves on the top of the box to block out light from a hanging lamp. These blocks were designed to block out light from two neurons at a time. We controlled the space between the sliding doors to show how exposure to light affects the neurons. We created a hole in the box to pass the piCobbler ribbon cable through, and attached the raspberry Pi
to the outside of the box using Velcro. We also drilled holes for 3 LEDs to be seen on the outside of the box. These LEDs were used to identify spiking of the left, right, and center neurons. The side view of our box can be seen in figure 11 to the right. Figure 12 shows the top view of the box with the sliding doors.
TFT Functionality
The piTFT essentially ran as a plug-and-play system on the Raspberry Pi. In order to get it working, we simply had to export the desktop monitor's framebuffer to our TFT screen and ensure that all environment variables were changed accordingly. Figure 13 below shows our working code on the TFT screen.
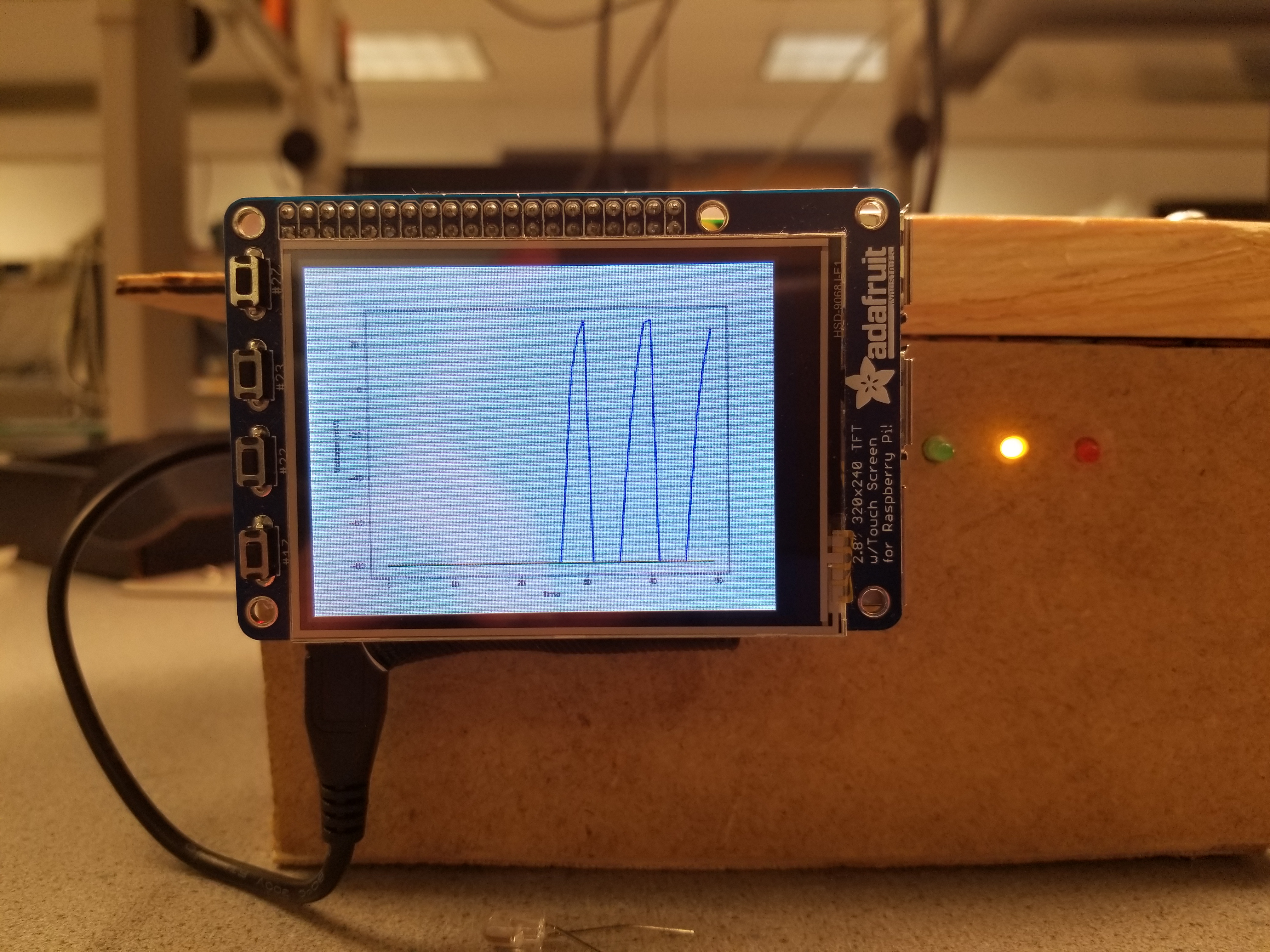 Figure 13: Working display of TFT on Box
Figure 13: Working display of TFT on Box
Startup on Power
Our final step involved creating a simple Bash script so that our program would run on bootup of the Raspberry Pi. This was done by including the python command to run the program in the rc.local file, and setting the command to run in the background.
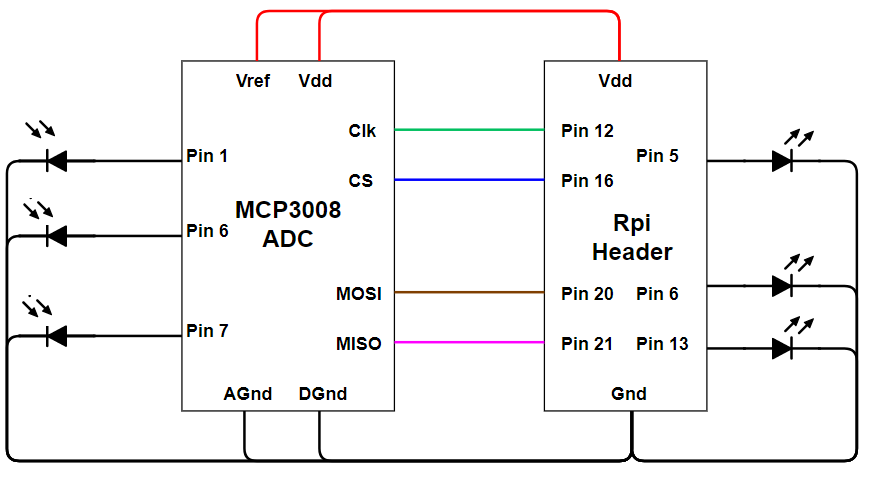 Figure 14: Final Schematic of Circuit
Figure 14: Final Schematic of Circuit
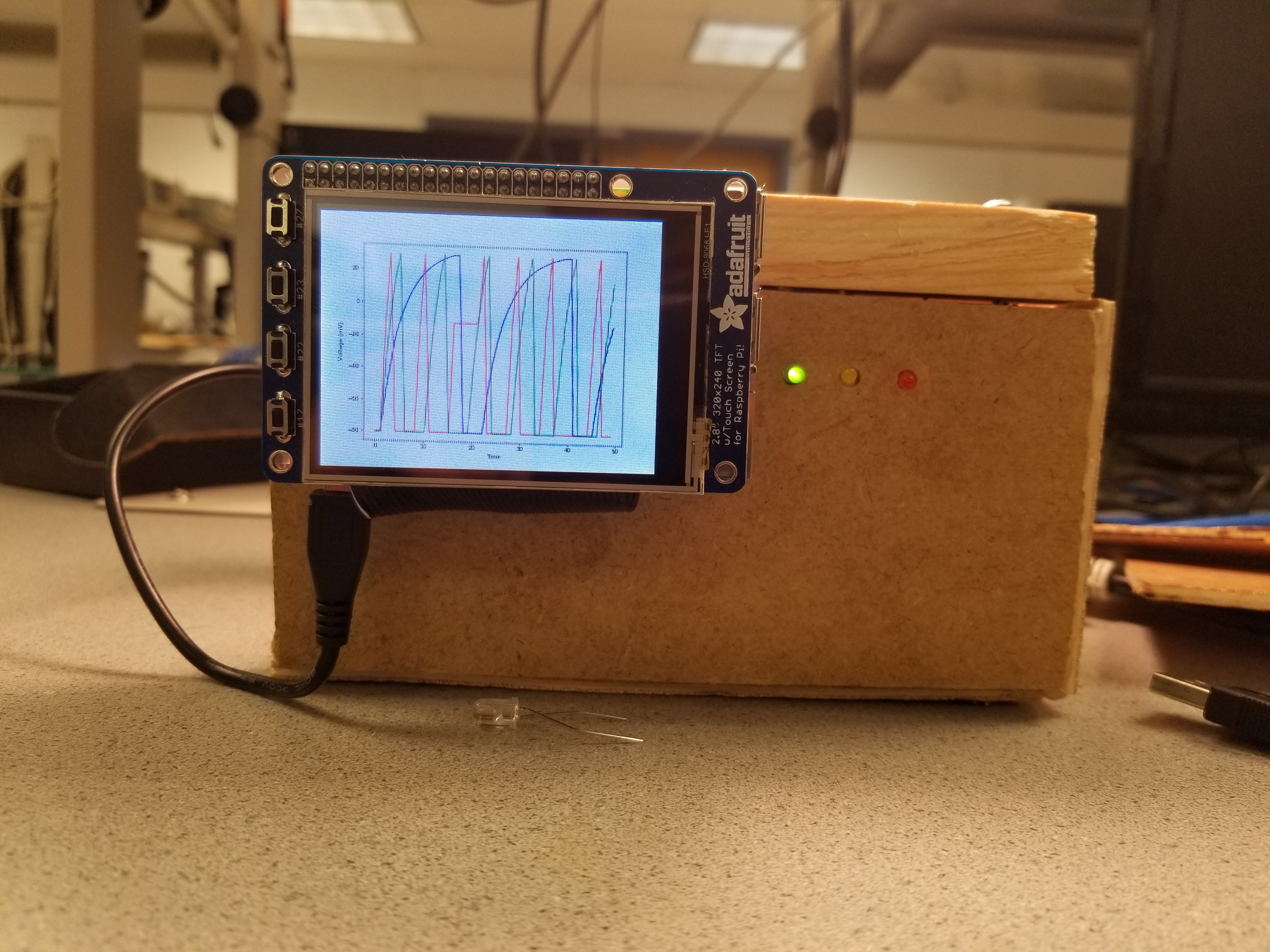
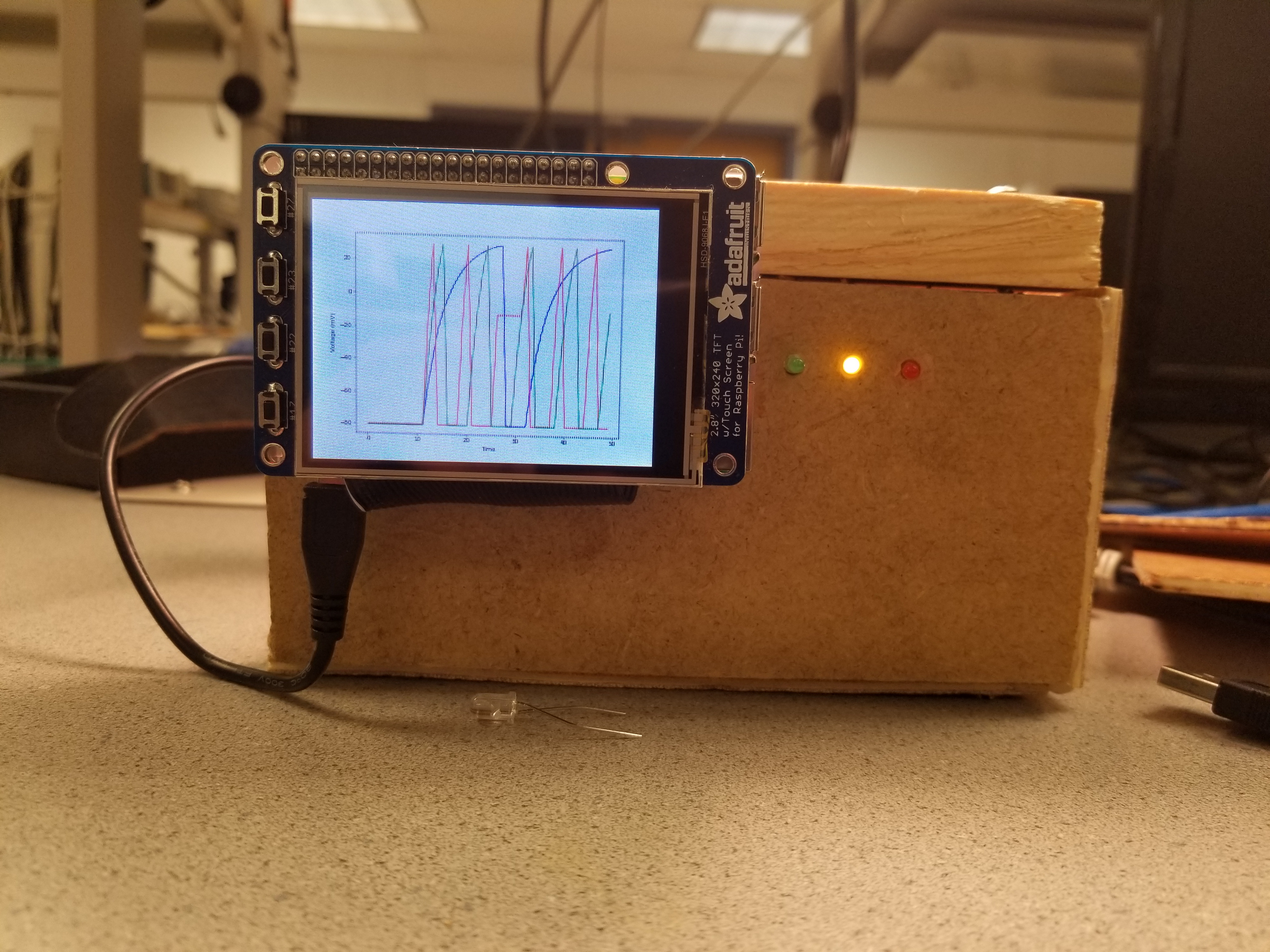 Figure 1: Functional Final Device
Figure 1: Functional Final Device 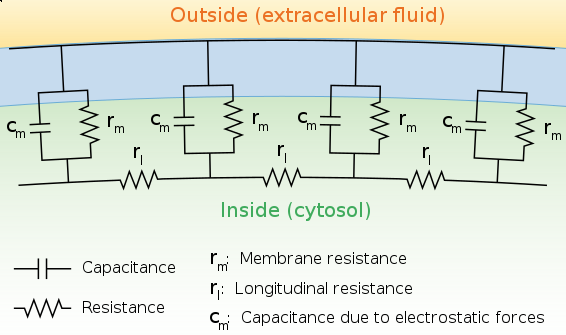 Figure 3: Cell Physiology
Figure 3: Cell Physiology 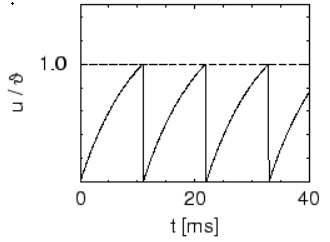 Figure 4: Exponential Integration
Figure 4: Exponential Integration  Figure 5: Optical Illusion through Lateral Inhibition
Figure 5: Optical Illusion through Lateral Inhibition

 Figure 13: Working display of TFT on Box
Figure 13: Working display of TFT on Box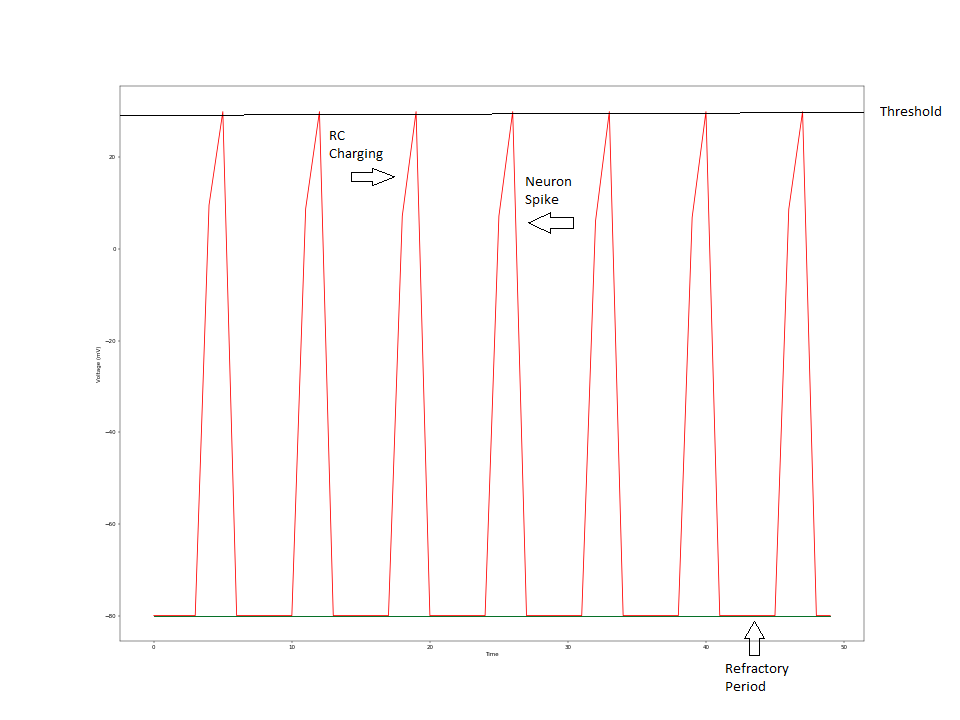 Figure 15: Isolated Red Neuron
Figure 15: Isolated Red Neuron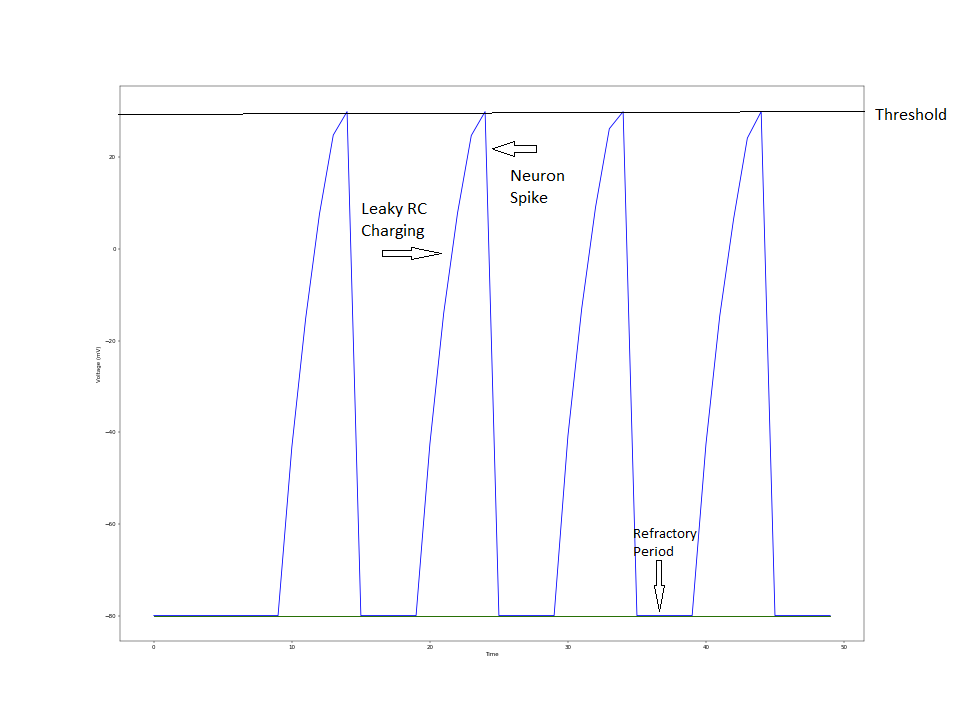 Figure 16: Isolated Blue Neuron
Figure 16: Isolated Blue Neuron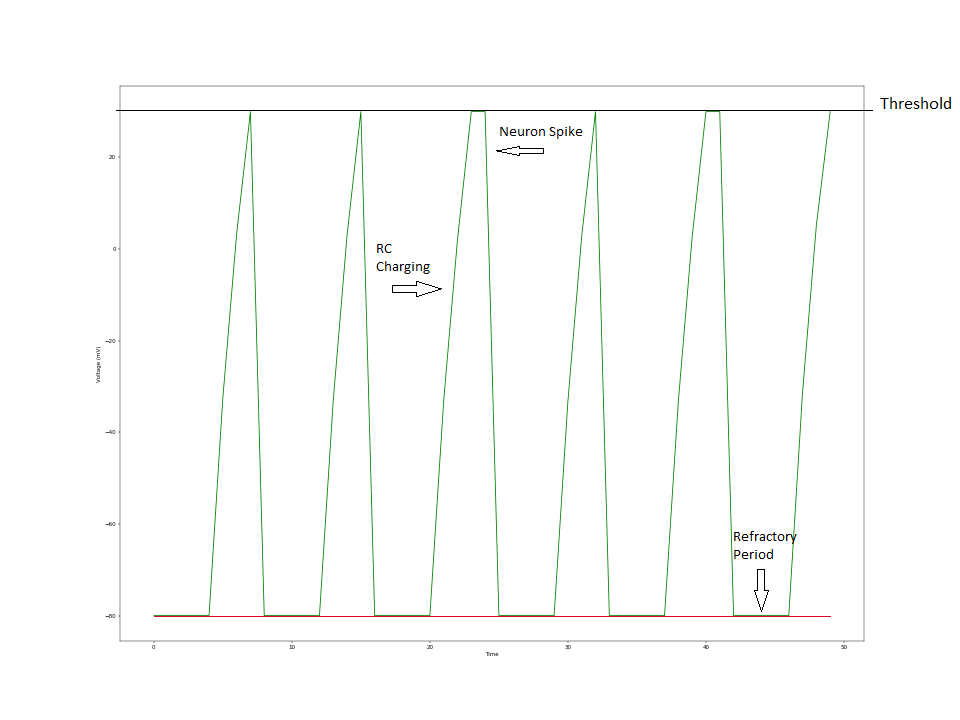 Figure 17: Isolated Green Neuron
Figure 17: Isolated Green Neuron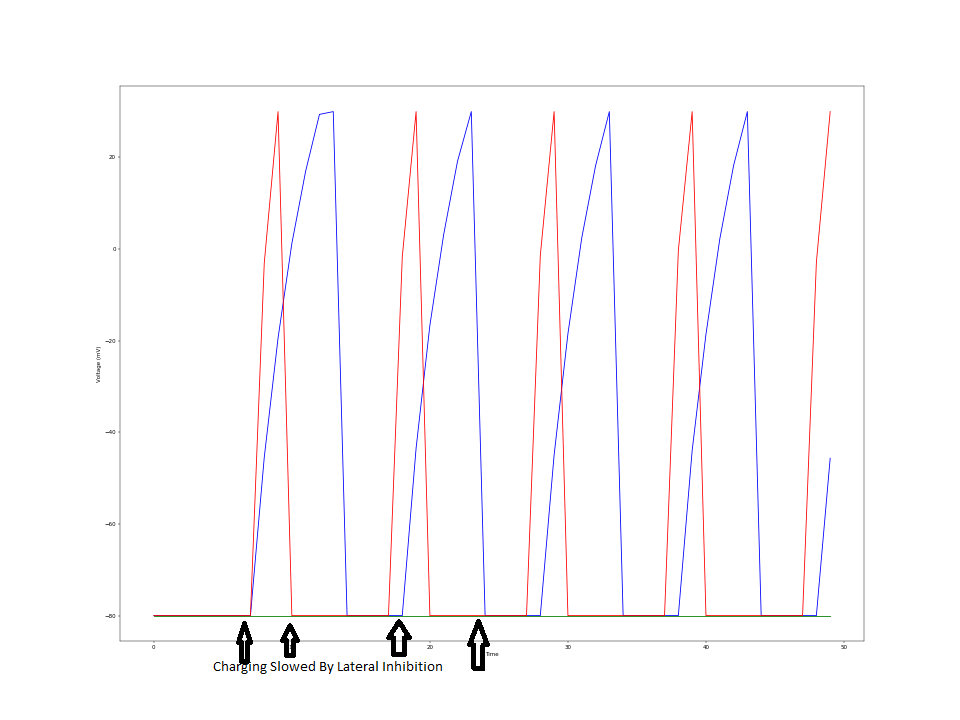 Figure 18: Red and Center Neurons Illuminated
Figure 18: Red and Center Neurons Illuminated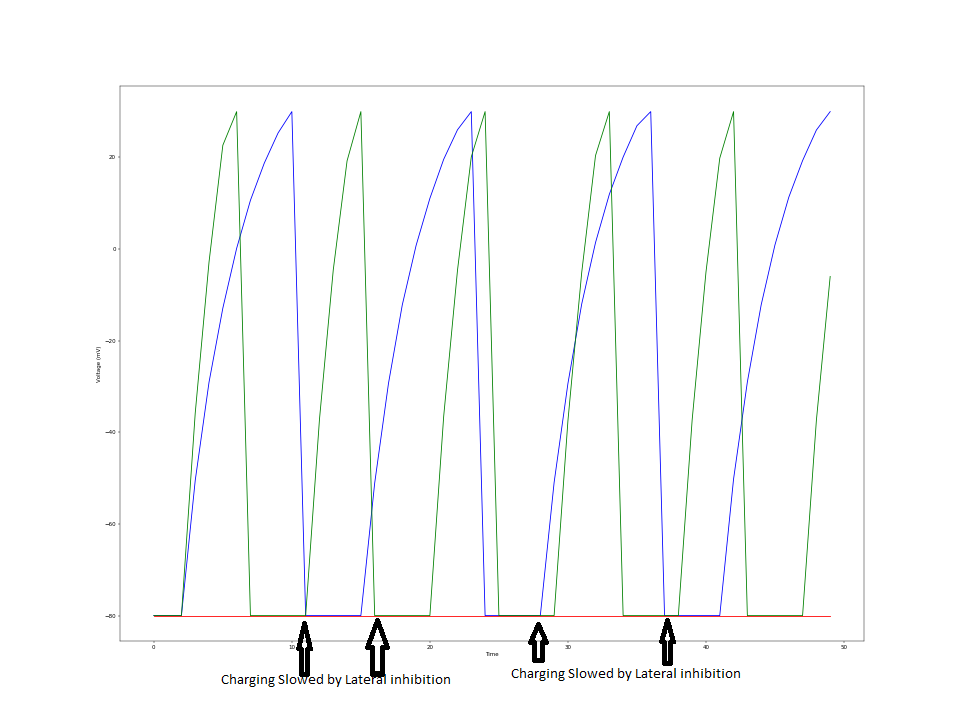 Figure 19: Green and Center Neurons Illuminated
Figure 19: Green and Center Neurons Illuminated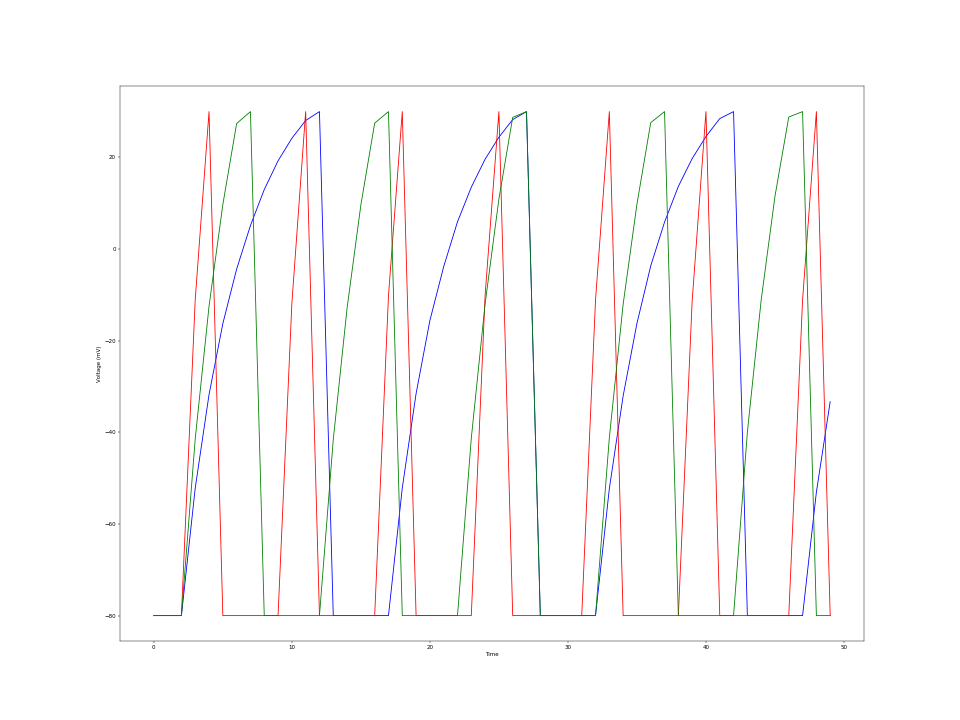 Figure 20: Voltage over Time for Neuron
Figure 20: Voltage over Time for Neuron