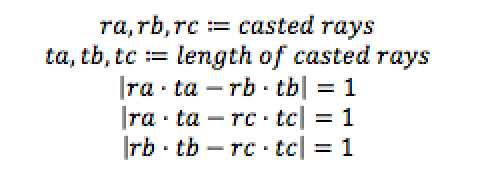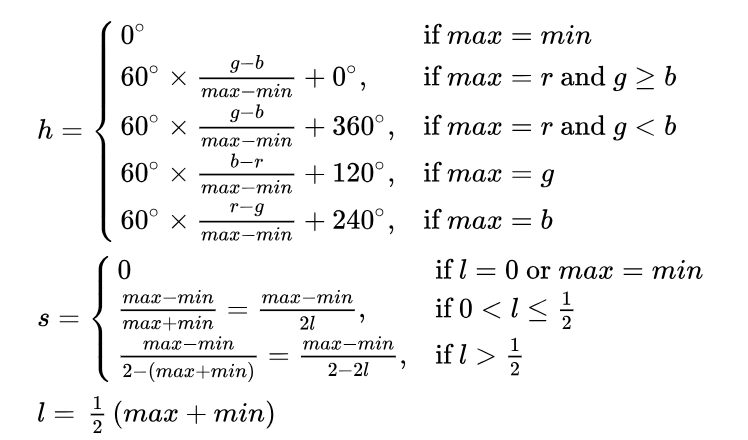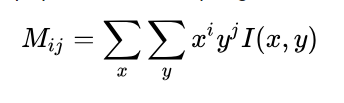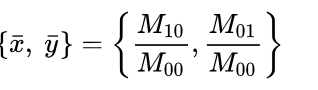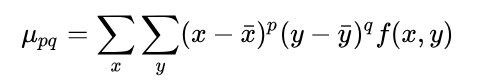Design
Overview
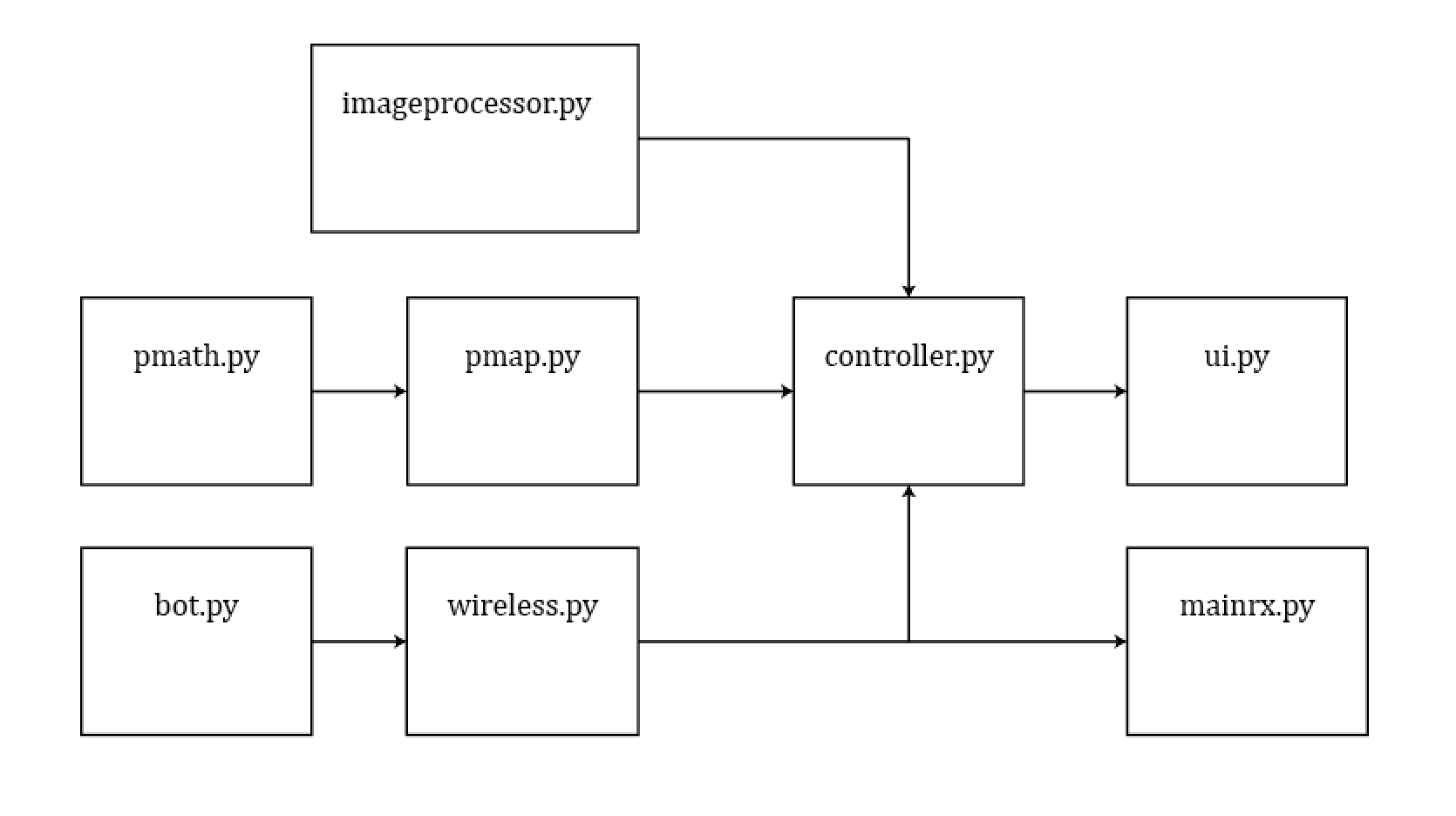
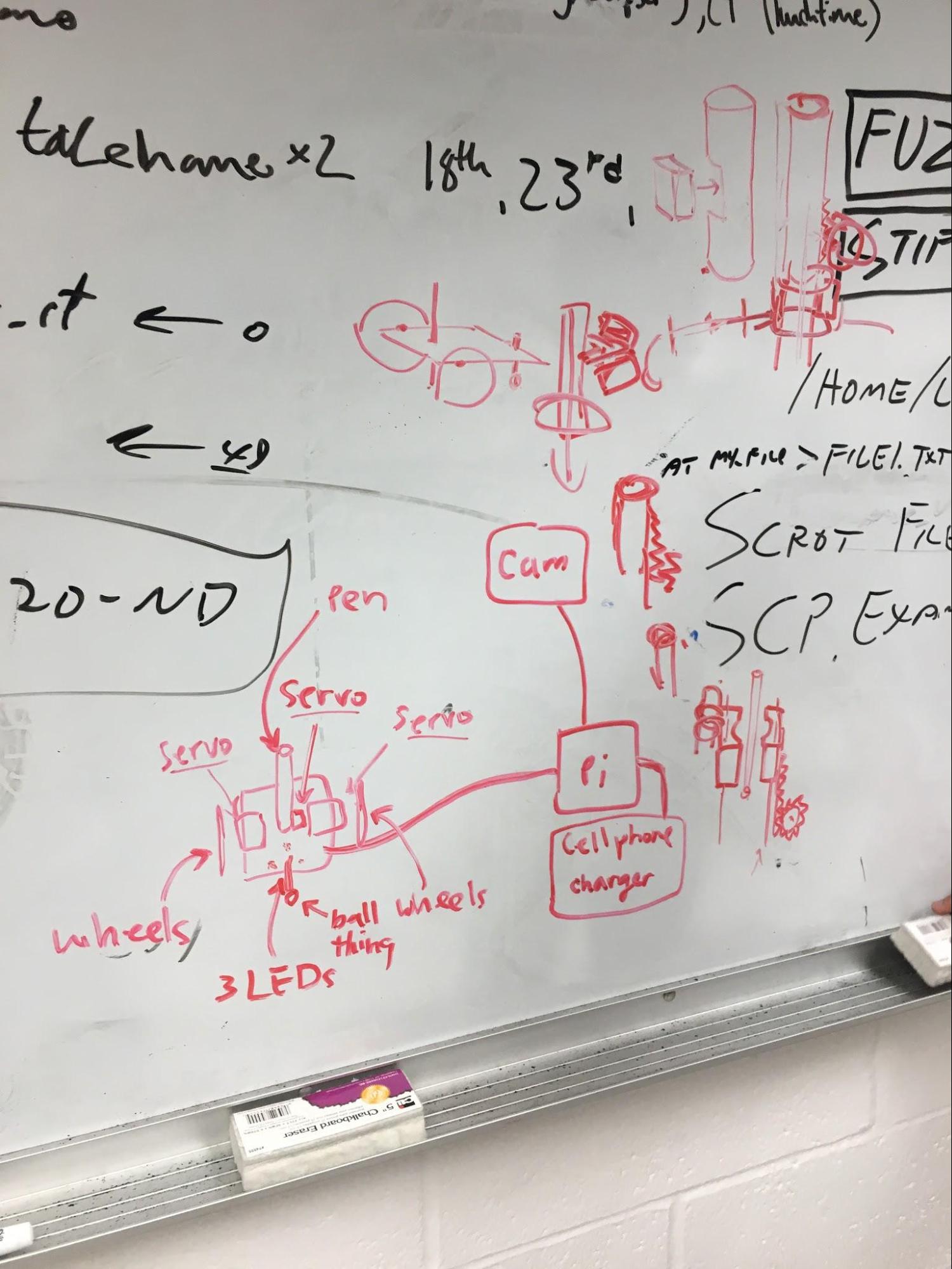
Because our project was fairly complex, we chose to implement standalone modules first, test to ensure the module was working correctly, then move on to implement modules that depended on this module. A high level diagram of the modules as well as the system of our robot can be seen below.
Figure 1: A high level diagram of the software. An arrow indicates an import.
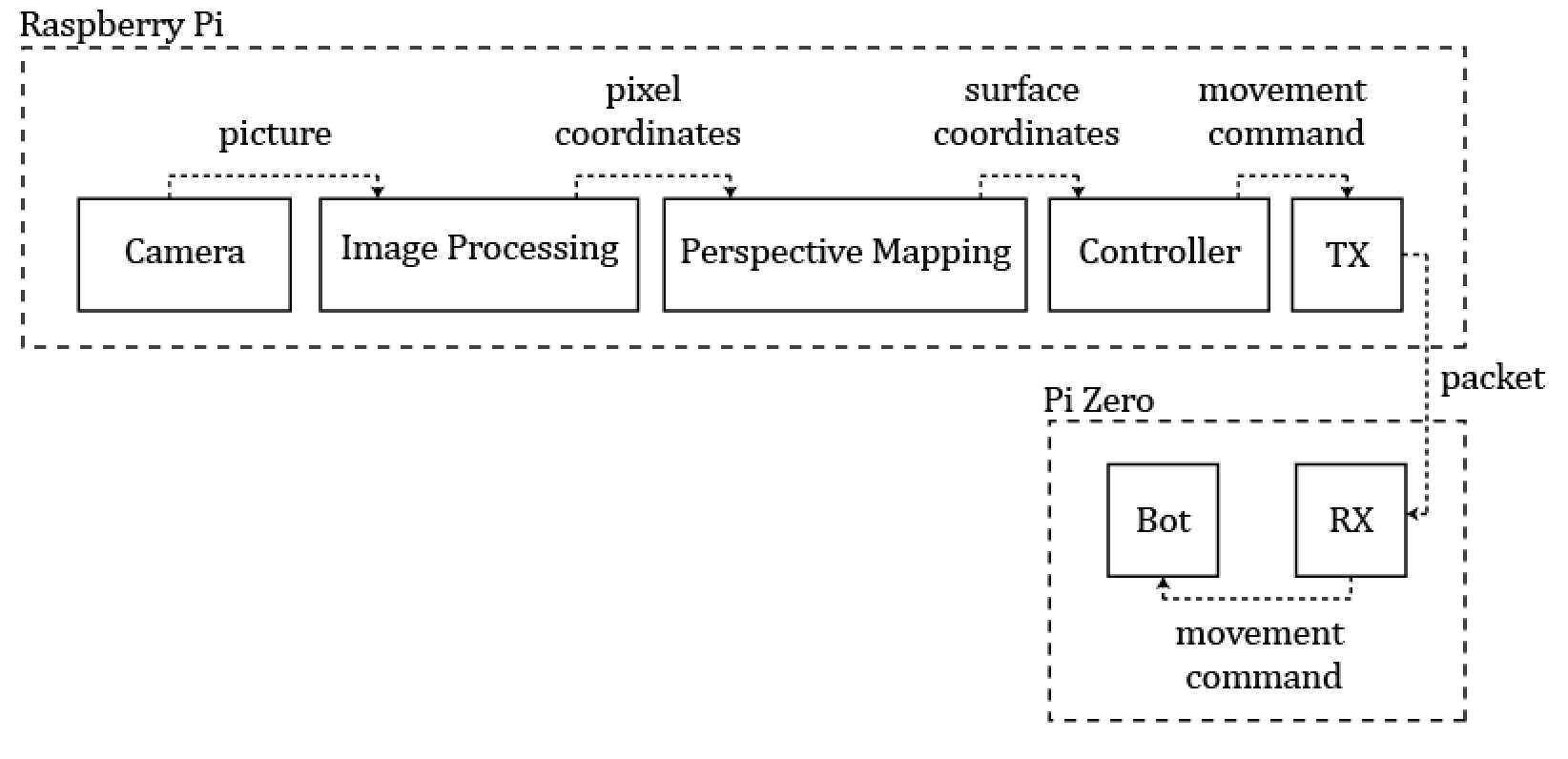
Figure 2: High level overview of how software components work together.
Our system works by first allowing the user to draw points on the PiTFT. When a point is drawn, it is automatically connected to the previous point with a line. After the user completes the drawing, the controller calibrates the perspective mapping software by having the robot move around in a predetermined fashion. Position of the robot is determined by a camera and three colored dots arranged in a triangle with a fixed distance of 1 inches between the centers of the dots. The drawn array of points is then sent to the controller which guides the robot from point to point, getting input from the perspective mapping software to determine the error in the bot’s trajectory and correct accordingly. The controller sends command packets to the Pi Zero (on the robot) via a socket connection to control the robot’s movements. Once the points are drawn, the user can decide to draw another picture for the robot to draw or quit the program. Each of these modules is described in detail below.
Perspective Mapping
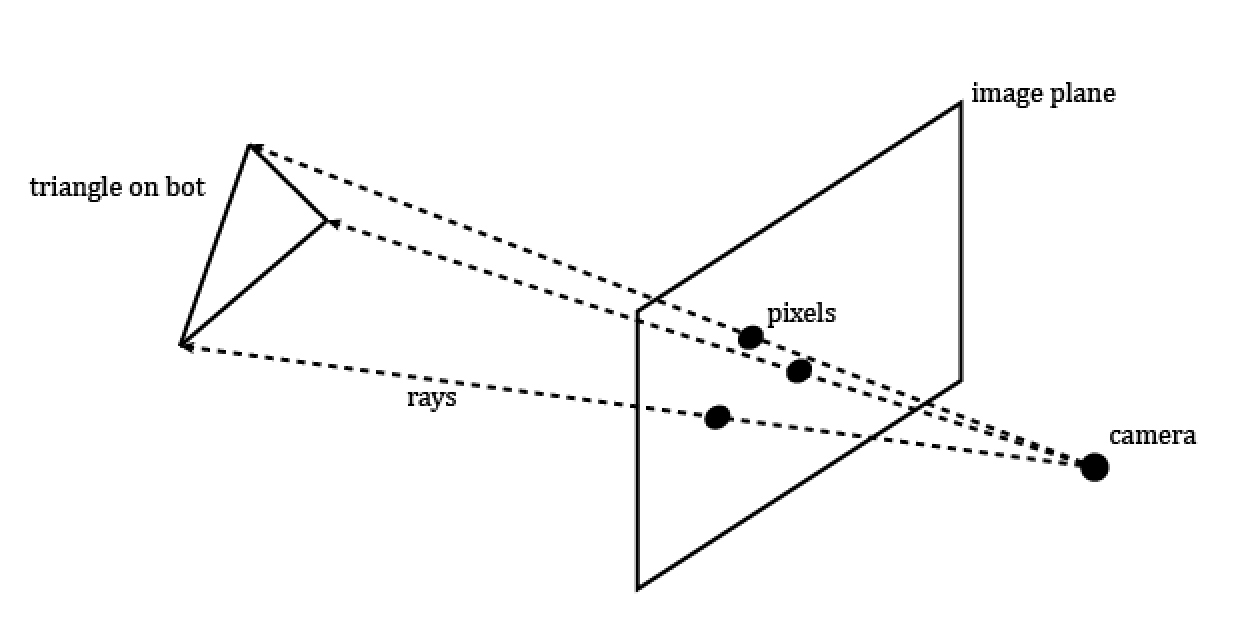
The perspective mapping code can be found in the file ‘pmap.py’ and the main job of this module is to take in 3 points specified by pixel coordinates and convert that into 3D positions in the real world. The way this happens is by using a technique in computer graphics known as ray tracing. Essentially, the scene is modeled by a point for the camera and an image plane in front of the camera. Using this model, a 3D scene of objects can be projected onto the image plane by casting rays from the camera (the beginning point of the ray), through a pixel, and onto the scene where it will hit some object. The color of that object is then projected back onto the pixel.
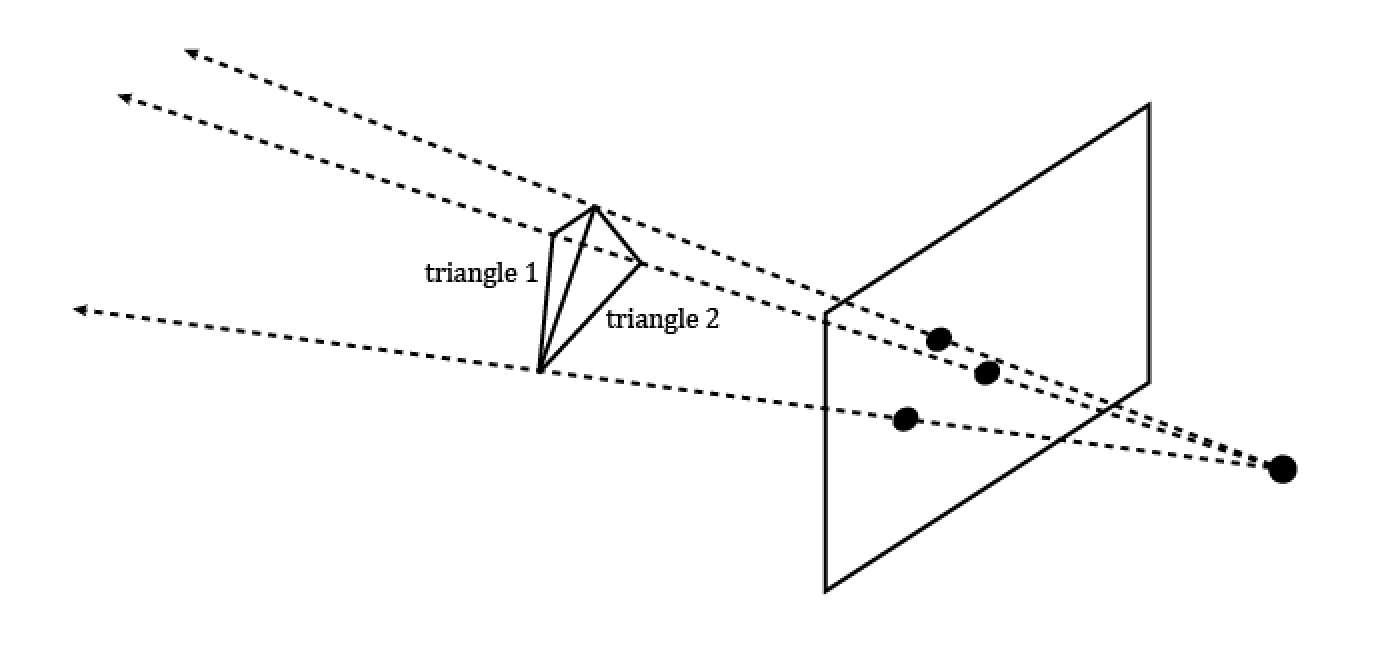
Using this technique in reverse, we can cast rays from the camera to the input pixels and determine where the ray intersected the scene. Below is a diagram to make things a bit more clear:
Figure 3: A simple diagram of ray tracing.
Because we know the distance is fixed between the sides of the triangle as 1 inches, this essentially boils down to a math problem of finding the likeliest length of the 3 rays with the 1 inch constraint. We can use the following equations (note that rays are represented as unit vectors):
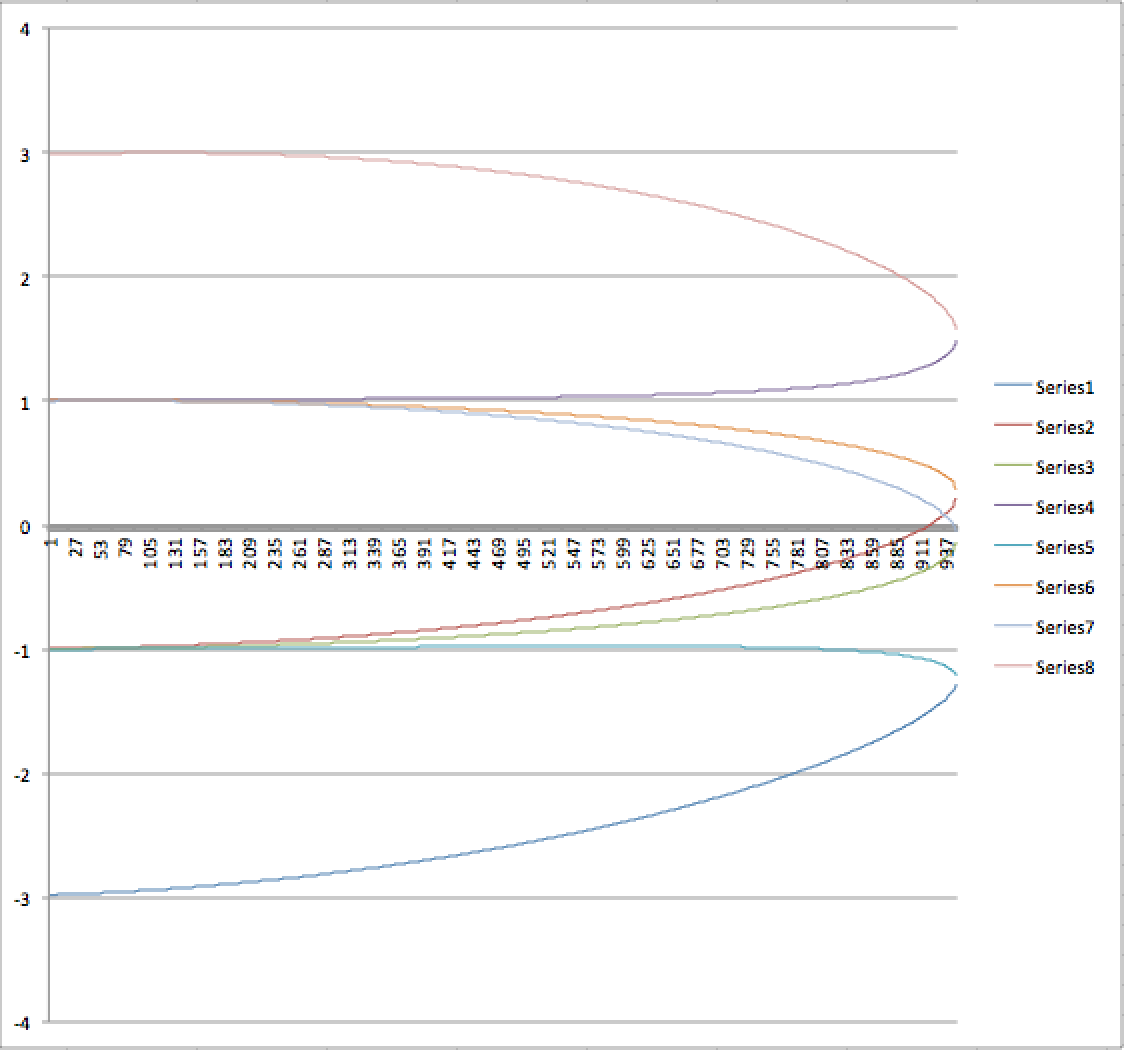
Our goal is to basically find the ta, tb, and tc values that satisfies the above equations. To do this, we implemented a function that sweeps ta , calculates the other length values based on this, and selects the ta value that yields a triangle that is closest to an equilateral triangle with side lengths of 1 inches. As it turns out, it is not quite enough to determine the 3D position of a triangle based on only the pixel coordinates: there are two solutions for each case. This is illustrated below:
Figure 4: Two possible solutions for the same pixel coordinates.
Figure 5: Graph of sweeping triangles. The y-axis here represents the error in upholding the condition that all triangle side lengths must be 1 inch and the x-axis represents the ta value. Two solutions can be seen where the error is nearly zero at x=~911 and another at x=~940.
Essentially, three points on a screen can be viewed as a triangle that is pointing towards you or a triangle pointing away from you. To figure out which of these was the desired solution, we needed to introduce some sort of calibration that would define the surface our robot was on and pick the triangle that was closest to the plane. Our calibration method takes a set of possible triangles and based on their surface normals, picks the surface normal that is closest to the most triangles in the set.
After the surface normal is established, future mappings become very easy since we simply need to intersect the rays with the surface to find the triangle. We can then determine the direction of the robot using the position of the three colors at each vertex of the triangle. Additionally, we use the first detected position of the robot as the origin of our coordinate system (which resides on the surface plane) and using the direction, determine plane axis vectors as well. Perspective mapping then becomes a O(1) operation and we simply need to solve the system of equations for ray intersection with the plane. We can then return the position and direction of the robot as 2D vectors.
One more component required to make this work was to take physical measurements of the setup. We needed to define a conversion factor from pixels to inches as well as measure the distance from the camera to the image plane. To do this, we simply took a picture of a ruler with the Pi camera, measured the distance from the camera to the surface the ruler was sitting on, and got the pixel to inch conversion factor by measuring the length of the ruler in the picture in pixels. The accuracy was not very important because we were mainly concerned with relative distances rather than absolute distances between points.
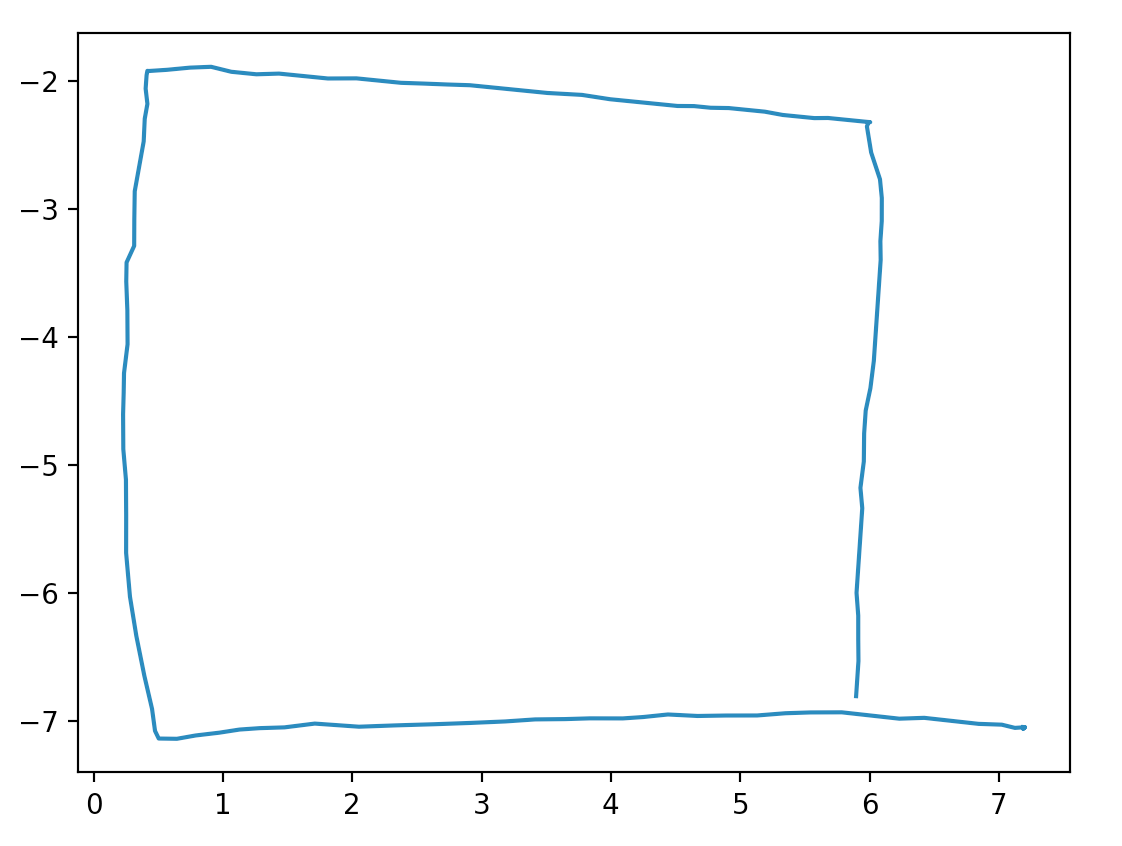
After this was completed, we tested by moving a paper on the table with three colored dots in a square in front of the camera and got the following result:
Figure 5: Perspective mapping, moving in a square.
Image Processing
The image processing code can be found in the file ‘imageprocessor.py’ and the main role of this module is to determine the position of the three colored dots on the screen in pixel coordinates by using the OpenCV library. To accomplish this, it needs to pick out the three colors reliably and ignore environmental noise that may be a similar color. We considered using LEDs since they are a light source and therefore would not be influenced by environmental factors such as dim lighting, but it turned out to be too bright for the Pi camera to detect as a color. We finally decided to print out 3 colored circles, 1 inch in diameter, on paper and place the paper on top of the robot for the camera to detect.
Our primary method of picking out the 3 circles was to use thresholding and generate binary images, one for each color. To do this, we specified the hue, saturation, and value ranges for each color and modified this across multiple tests to ensure that it worked for a wide range of environments while also minimizing the amount of noise present. Additionally, we needed to convert the input image from the standard RGB to HSV. Below is a table of the threshold ranges for each of the circles as well as the conversions to HSV:
Table 1: Hue, saturation, and value ranges for thresholding. (Note: hue values range from 0 to 179 while saturation and value range from 0 to 255).
Figure 6: Equations to convert from RGB to HSV
Figure 7: convert actual image from RGB to HSV
Much of this was trial and error, first testing for the nominal, well lit case and then moving on to shadowing the circles to see if it still worked. We found that converting to HSV helped a lot because hue would be constant regardless of the lighting conditions. One problem we encountered while testing was that depending on the time of day, there was varying levels of yellow and blue in the environment, namely a lot of blue and yellow that was highly unsaturated. To correct this, we adjusted the saturation so that those values would be cut out of the image.
Once binary images were produced, we needed to first filter out noise and locate the position of the three circles. To filter out noise, we first used OpenCV to find the contours of all the shapes in the binary image, and cut out contours which were below a specified size limit. We were then able to use moments to find the most circular shapes, as shown below:
Figure 8: Moment equations
We then got the top three candidate circles for the binary images of each color (9 total), looked every possible combination of circles, and selected the group that was most tightly packed (closest together). Once the circles were determined, we again used the moments function to determine the centers of the circles. With this process, we were able to reliably locate the three circles in any lab lighting conditions and return their centers.
Wireless Communication
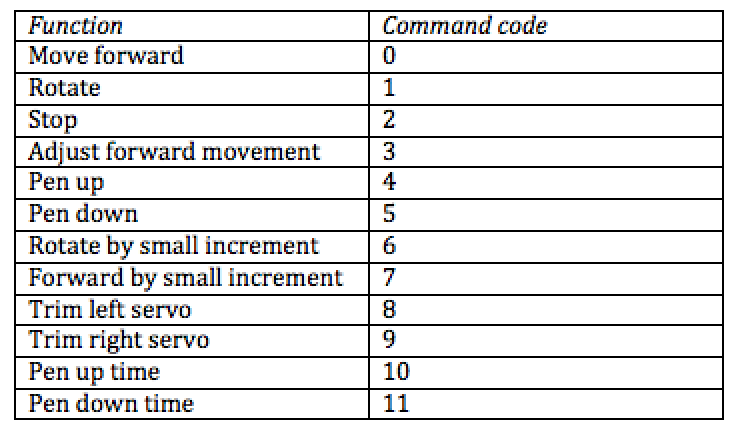
The job of the wireless communication module, found in the ‘wireless.py’ file, is to provide an interface that allows the Pi to communicate to the Pi Zero and remotely control the robot over the WiFi. It does this by establishing a TCP connection via the python socket module. The Pi acts like a server and sends commands as strings via a command code followed by a single argument for that command. The receiver then receives these commands one by one, looks up the command code, and executes the correct function on the actual robot. Below is a table of command codes we used for our robot:
Table 2: Commands and their command codes.
Additionally, because the receive method of our socket blocked until it received the specified number of bytes causing erratic behavior, we specified a packet size of 50 bytes and executed commands one by one with no buffer (our connection was fast enough that commands were sent almost immediately). Our main concern for this was possible latencies between the server and the robot but because our packets were fairly small, we did not experience any noticeable delays.
Bot Controller
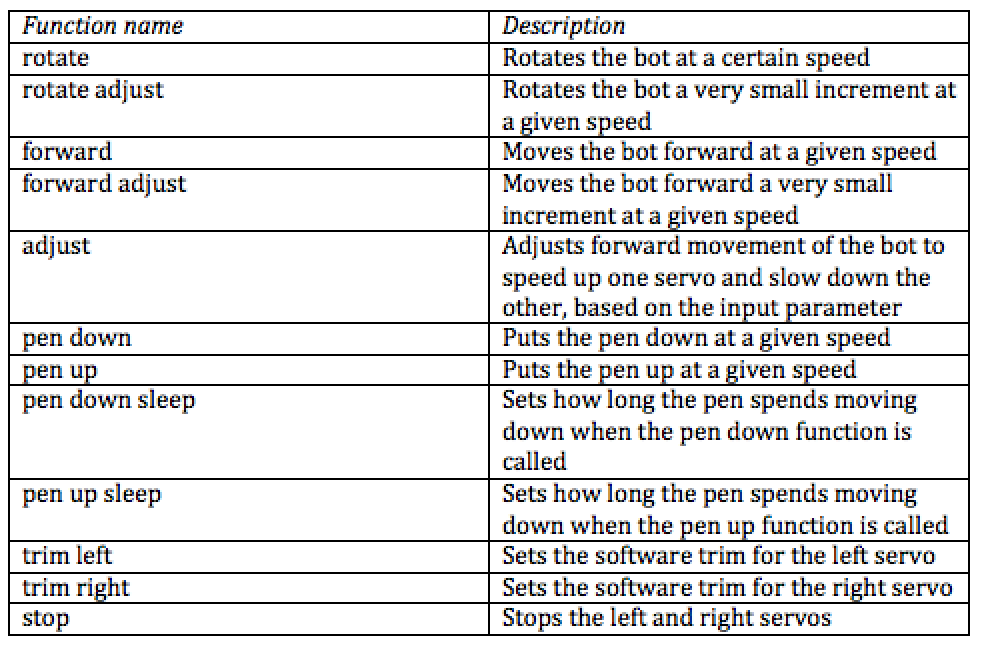
The job of the robot controller is to provide a library of functions that is able to move the robot in a variety of ways and can be found in the file ‘bot.py’. The robot itself is fairly simple, consisting of only 3 continuous rotation servos, two for the wheels and one for moving the pen up and down.
We first created a servo class that encapsulated functionality of a single servo. Our initial implementation consisted of using software PWM to control the servos, but we quickly realized that we needed to control the speed of the servos as accurately as possible. Due to this, we switched over to a hardware PWM implementation which greatly improved robot movement. The bot class provides several functions for moving the robot and their uses will be further discussed in the main controller section. Below is a table describing each function:
Table 3: Table showing all functions of the bot class.
One of the main issues with the bot was getting the pen to draw reliably and as much in the center of the bot as possible. In our first iteration of the bot, the servo would push the pen down while also pushing the whole bot up so that the wheels were not touching the ground. To fix this, we needed a weight of some sort so we placed a rock on top of our bot to hold it in place. This also provided more friction between the wheels and the paper which improved mobility. Our bot can be seen in the figure below:
Figure 9: Pictures of our bot. The rubber band can be seen on the right and the rock can be seen on the left, providing a weight to hold the pen down.
Main Controller
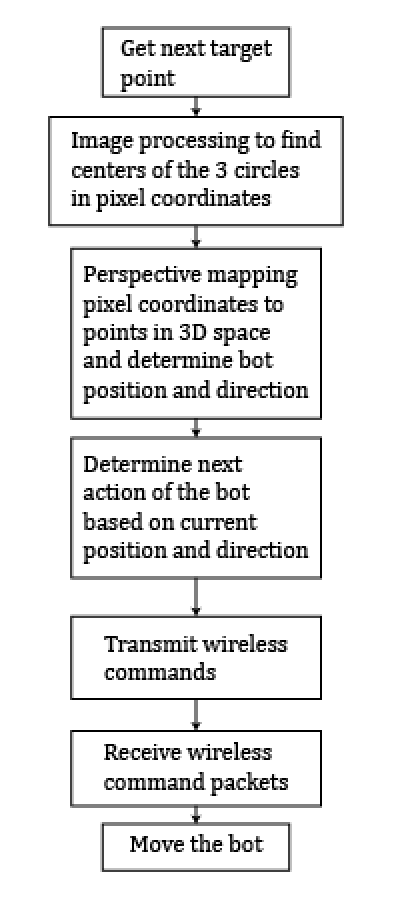
The main controller (found in the file ‘controller.py’) is responsible for using the library functions provided by the image processor, perspective mapping, and wireless bot to guide the robot from point to point. Additionally, the controller contains all of the parameters for bot movement such as servo trimming, error tolerances, bot speed, and so on.
The controller first establishes a wireless connection with the bot, and calls functions that sets up static parameters of the bot including trim values for the left and right servos, pen up and pen down speed, and the length of time spent putting the pen up or down. After this, it starts a calibration routine that basically moves the bot in a predetermined sequence so that the perspective mapping software can determine the surface normal of the plane on which the bot is on. Once completed, the perspective mapping software can identify the position of the bot using the established surface normal and surface axes. The controller then starts the sequence of moving from point to point. A diagram of this process can be seen below:
Figure 10: Main sequence of events to draw from point to point.
As shown in Figure 10, triangle pixel coordinates are obtained from the image processor which is then passed to the perspective mapping to determine the position and direction of the bot on the surface plane and based on this information, the next movement of the bot is determined.
The movement of the bot was especially difficult since drawing needed to be as accurate as possible. To accomplish a high level of accuracy, we implemented a variety of tweaks: to move to a certain target point, the bot is rotated to within a certain tolerance (fairly large, about 40 degrees) towards the target point and then is rotated thereafter in very small increments until the target direction is reached. We only rotate in one direction since the servos are not perfectly calibrated (since they were both cheap and naturally have small differences in movement speed) and may rotate inaccurately in one direction but accurately in the other. We also increment in small amounts until we have just passed the target direction which we check by looking at the sign of the cross product between the two vectors. Moving forward works the same way where we move the bot forward towards the point to within a certain radius and then move forward in small increments until the target point has been just passed. We check this by looking at the sign of the dot product between the target direction and the bot direction.
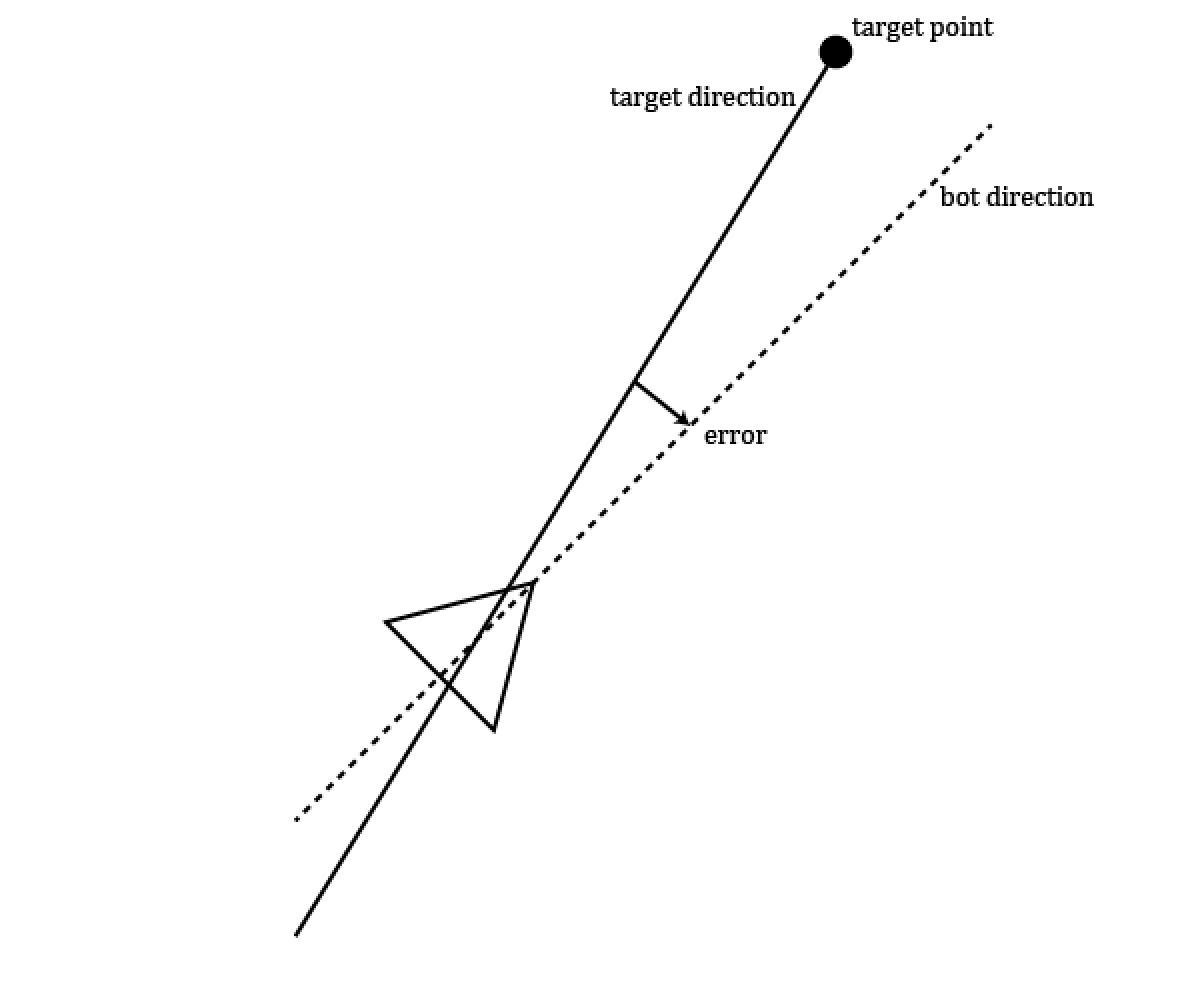
Additionally, we implemented a variation of PID control (using just the proportional component) to guide the bot while it covers the distance to the target point to within a certain radius. Our error is based on the angle difference between the bot direction vector and direction vector from the bot to the target point. Based on this error, one of the servos is slowed down slightly while the other is sped up slightly to correct the error. We considered adding in the derivative and integral components but found that using only proportional worked well.
Figure 11: Diagram showing error for proportional control.
One of the main problems we had with the bot was the rate at which it could complete the sequence shown in Figure 10: often times, the overhead of the image processing and perspective mapping was enough for the controller to stop the bot later than desired, causing the bot to overshoot the desired location or direction. The reason we used the small rotational and forward adjustments was to correct this problem. We initially tried to decrease the servo speed but found that the slowest speed possible was still too fast for the system to catch it and stop it in time.
User Interface
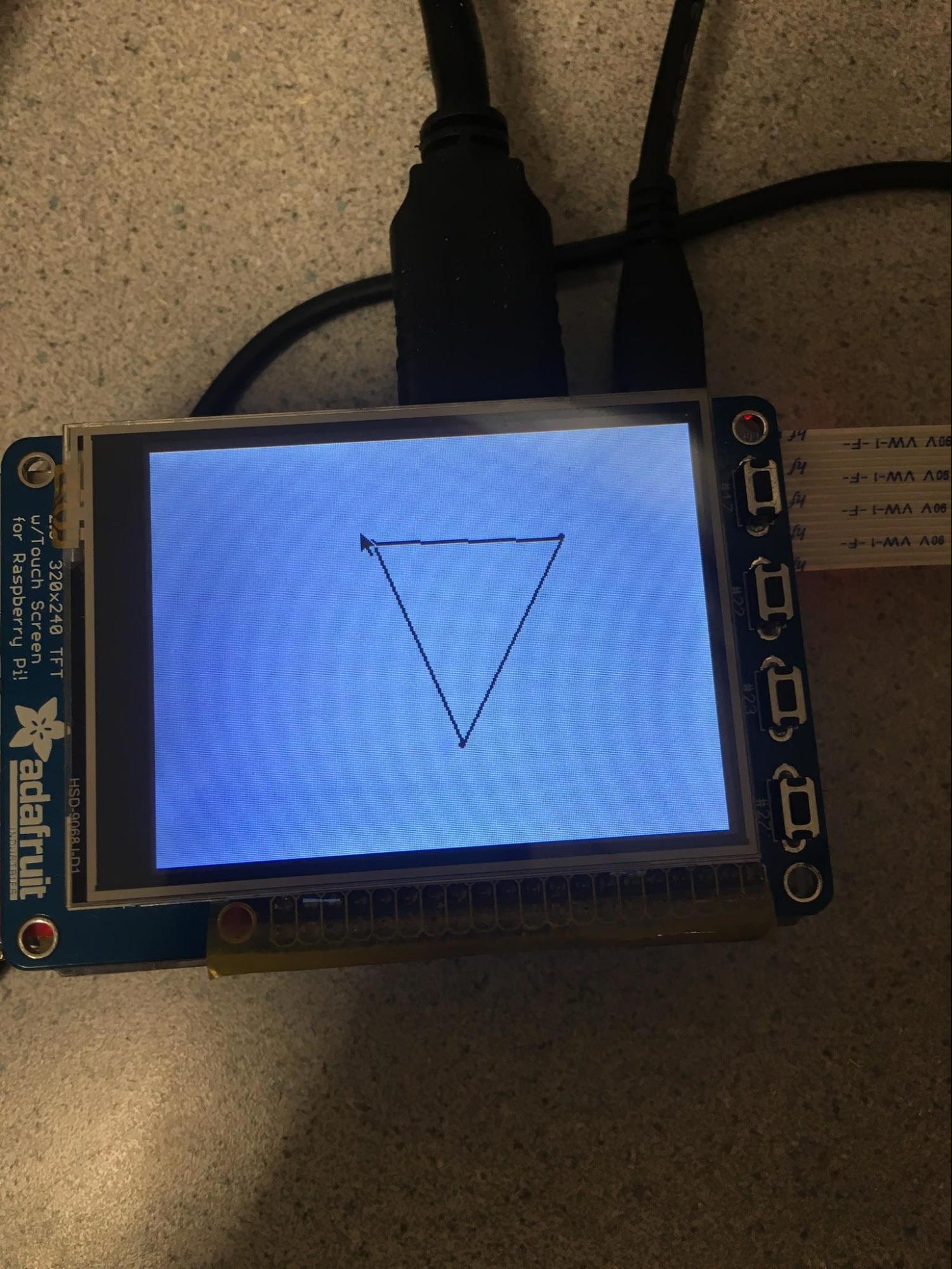
The user interface code can be found in the file “ui.py” and essentially creates a simple interface on the PiTFT for the user to draw shapes. The user can use the 4 buttons to clear the drawing or quit the program (when there are no points), redo, undo, and complete the drawing and start drawing. Points can be placed on the canvas by using the touchscreen of the PiTFT. After the drawing is completed, a point array (of pixel coordinates) is passed to the controller and the bot begins drawing. The UI can be seen below:
Figure 12: Picture of the user interface.
Figure 13: Another picture of the UI. The clear button changes to a quit button when the canvas is empty.
Figure 14: Side button text disappears after a few seconds of not pressing any buttons.