Self-Balancing Robot

a ECE 5725 Final Project
by
Alex Lui (al754) and Jordan Brunson (jdb429)
Fall 2018

Introduction

Anyone who’s seen Boston Dynamics videos cannot help but be awestruck (and maybe even a little terrified) of the incredibly graceful and lifelike movement exhibited by their robots. Mobile robots such as these are dynamics and controls masterworks. Drawing inspiration from such great feats as these we thought it be appropriate to try to develop a self-balancing mobile robot. Such a robot, we envisioned, would not only be able to balance itself but also navigate based on user command and do all this while carrying other objects. This, we figured, could be accomplished with a balance control algorithm running on a Raspberry Pi. The balance control would receive orientation data from an accelerometer/gyroscope chip and would issue commands to a motor driver thereby controlling the wheels at the base of the robot. This seemingly straightforward idea would end up becoming a monumental undertaking. Throughout the following page we detail our first ever attempt at creating a self-balancing mobile robot.

Project Objective

The goal of this project is to develop a two-wheeled standing robot that balances itself using its base wheels. This robot should be able to balance while holding an assortment of other objects. Furthermore, it should be able to maneuver forward, backward, left, and right based on a received command. These features will be controlled using a Raspberry Pi.

Design & Testing

The design of the self-balancing robot involved the development, calibration, and troubleshooting of quite a few subsystems and subassemblies (see below list). Despite their coupled nature, each will be discussed individually before elaborating about the system as a whole.

Robot Frame

To hold all the components together, a frame had to be developed. The developed frame would have to be rigid while also being accessible. Since we would be using 3D printing, the designs that we would come up with could be complex if needed. One of the initial designs (see below), would have had all the components stowed away compactly in the robot frame.


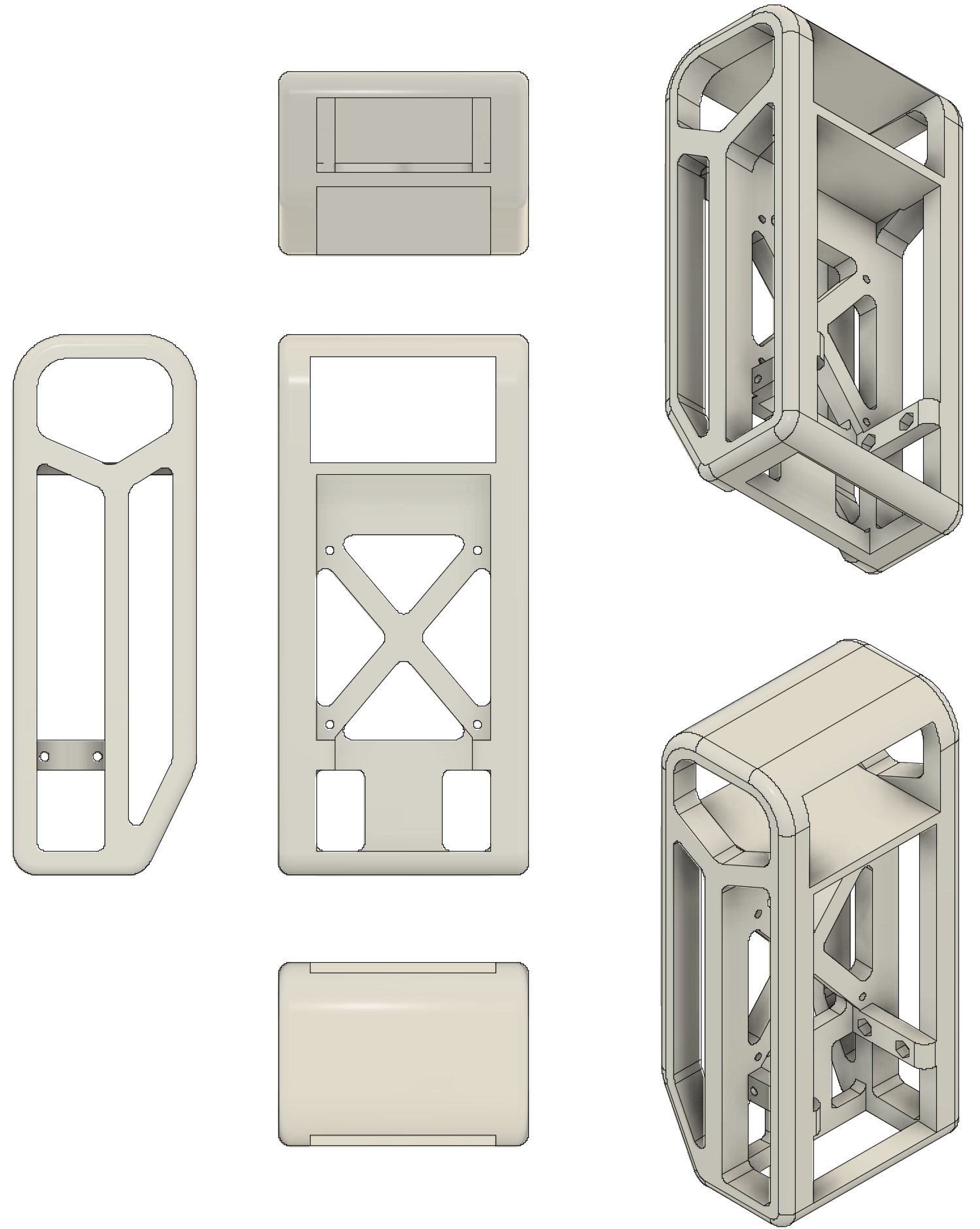
first design image

This design ended up being discarded as there was concern over the vertical mounting of all the components and the lack of flexibility in the design. A new design was envisioned that would use a shelf system to hold all the components of the robot. This way the components would be mounted horizontally and, if more space were needed, more shelves could be added (flexibility). The design consisted of a base unit (see below) which would serve as a connection point between the DC motors and the shelf assembly.


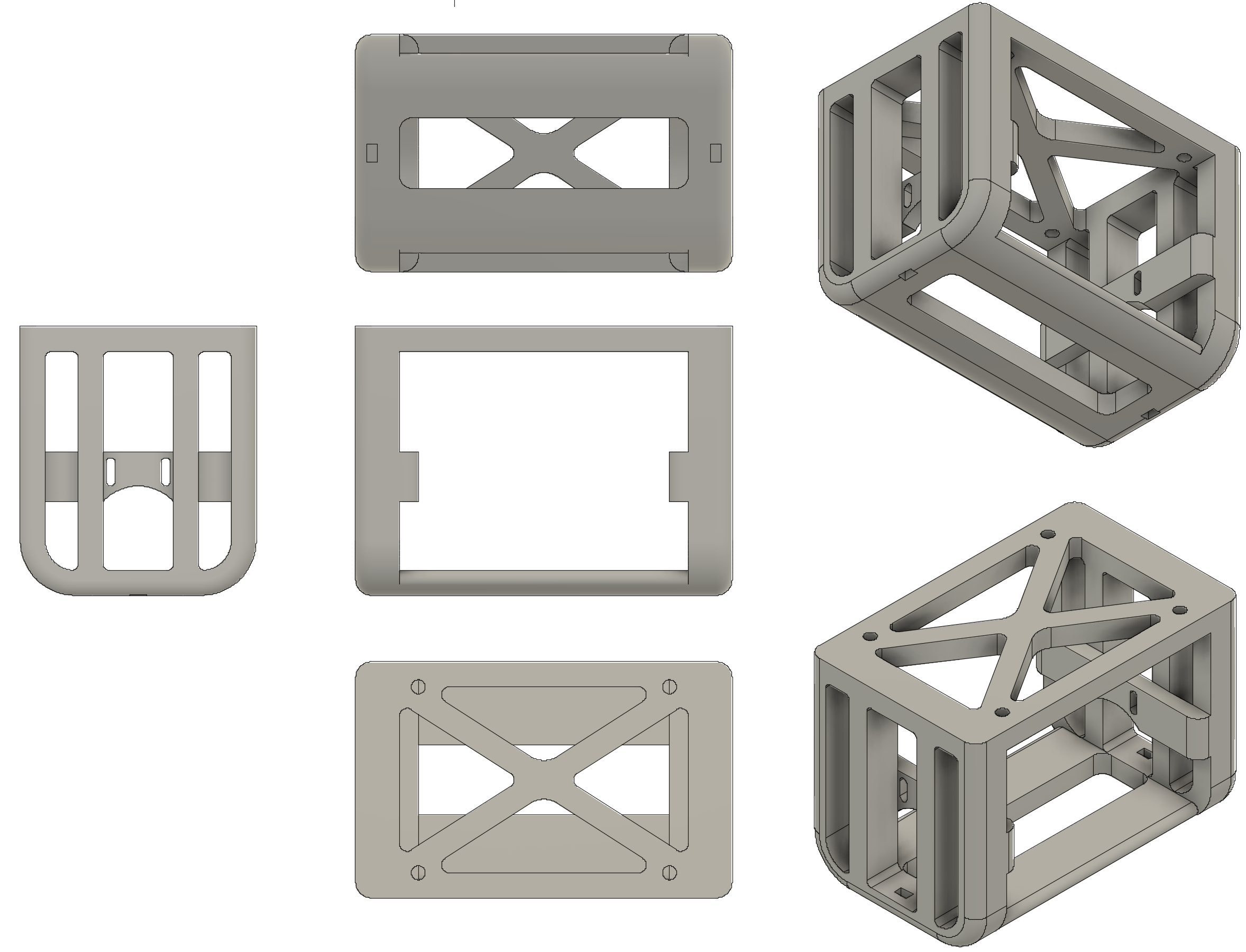
second design image

After 3D printing the base unit, a shelf assembly was created using a 0.25” wood sheet and some threaded rod. The robot frame was then fully assembled(see below). At the suggestion of our TA we also installed several "training rods" to the base unit of the robot. These prevented the robot from falling hard on one of its faces. This proved especially useful during the controls tuning phase.


full frame image

Sensors

Before any balance control algorithms could be developed, a sensor was needed in order to establish the robot’s orientation in space. Determining an orientation requires the use of either an accelerometer, a gyroscope, or a combination of the two. The good news is that accelerometers and gyroscopes are often sold together on the same chip. As it would later turn out, not all accelerometer/gyroscope sensors are equal. This was unfortunately discovered well into our project and led to much frustration.

LSM9DS1

We initially opted to use Adafruit’s LSM9DS1 which contains a 3-axis accelerometer as well as a 3-axis gyroscope. This sensor was particularly appealing due to its relatively lower cost. Once the sensor was received it was wired up (see below) and was mounted to robot frame.


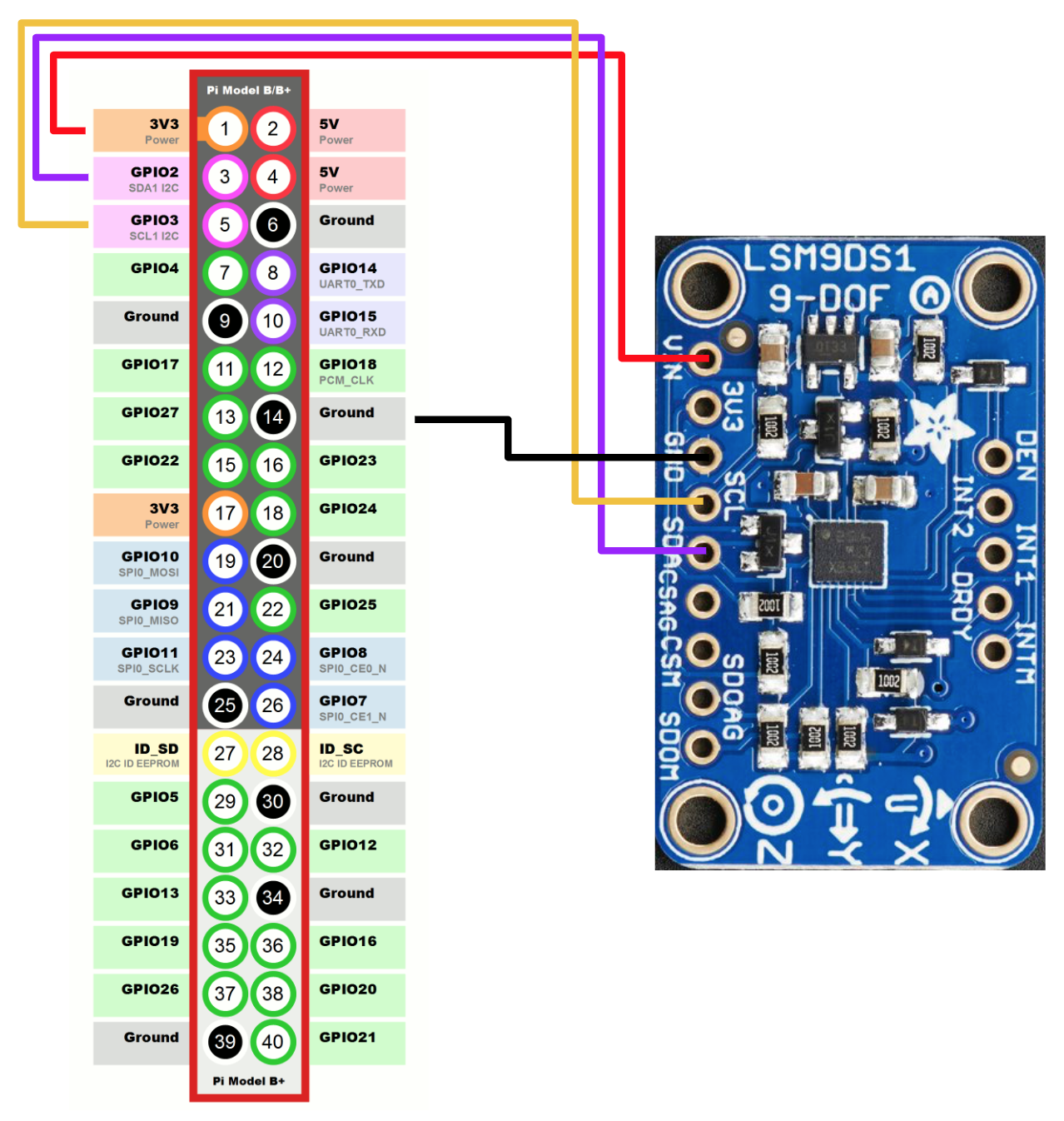
lsm9ds1 wiring
Images courtesy of raspberrypi.spy.co.uk and adafruit.com

At the time it appeared that the LSM9DS1 prefered to interact with c language as opposed to Python. In order to access the LSM9DS1 data stream, we installed the LSM9DS1 Raspberry Pi Library by SparkFun which, given our best understanding, acts as a Python-c interface (this may not be accurate). As we would find out later, accessing the LSM9DS1 datastream could be done with the Adafruit’s CircuitPython Library.

Fortunately and unfortunately, as our project progressed to its final stages, it was realised that the LSM9DS1 was delivering very noisy data compared to other commercially available accelerometers/gyroscopes. This was understood after countless hours of perplexion over why our robot was so bad at balancing. In addition to the noisiness of the measurements, all accelerometer data received from the sensor was a measurement of the total perceived acceleration. This meant that in addition to the perception of the gravity vector, the accelerometer would also pickup the other accelerations caused by the pendulum swinging motion and the acceleration of the wheel base. Such acceleration measurements cause the balancing algorithm to mistake its true orientation. While it was good that we were able to identify the suboptimal component, it was sad that it happened so late.

BNO055

In order to combat noisy accelerometer and gyroscope measurements, we acquired the BNO055 from our beloved TA, Xitang. Beyond the cleaner measurements, this sensor has the built in capability of measuring absolute orientation. This was a much welcome feature as it eliminated the need to include acceleration corrections in our balancing algorithm. The only downside to the new sensor was substantially higher cost (more than double the cost of the previous). The BNO055 sensor was wired up (see below) and was mounted similarly onto the frame of the robot.

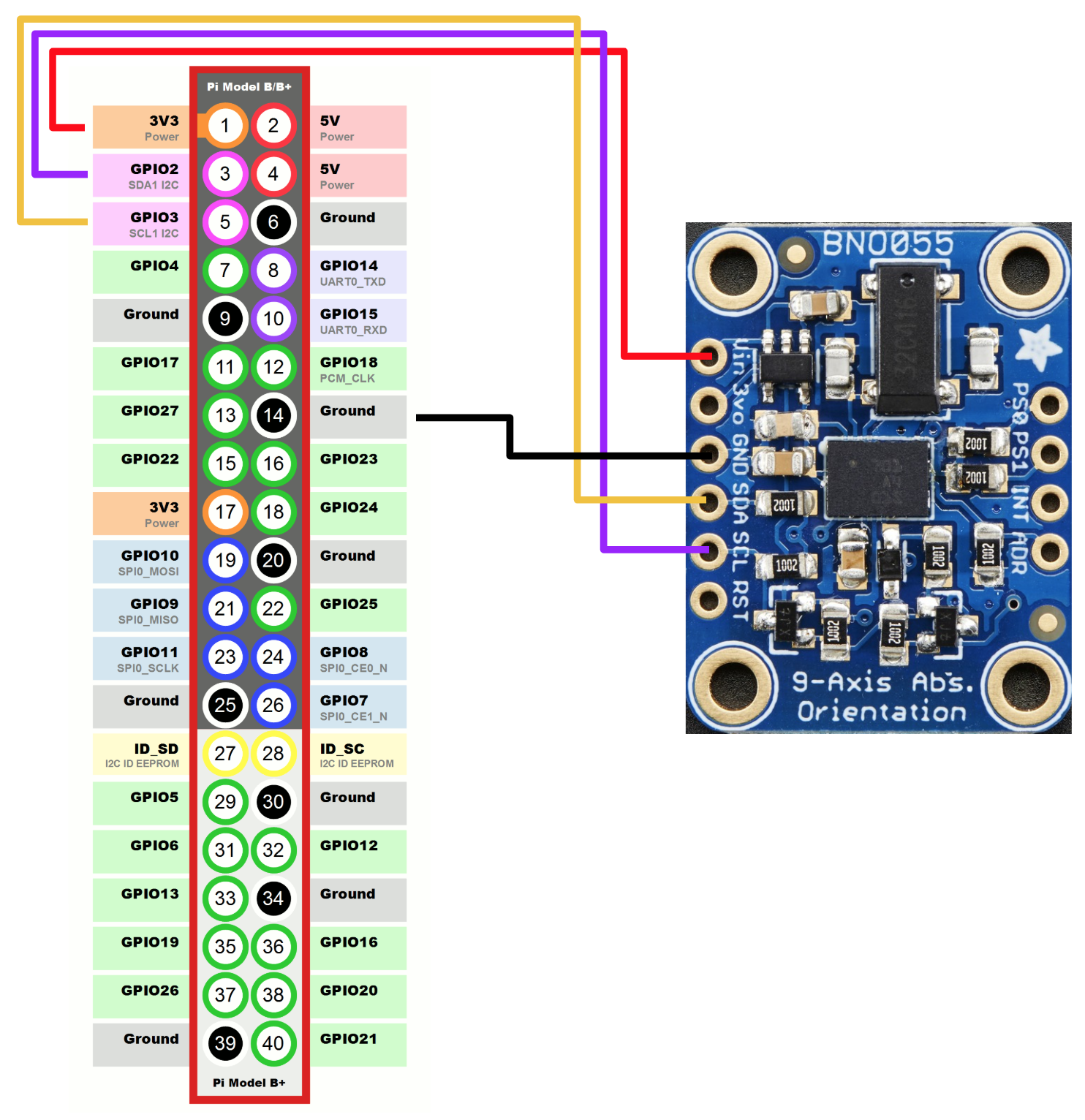
bno055 wiring
Images courtesy of raspberrypi.spy.co.uk and adafruit.com

Motor Control

The mechanism that fundamentally keeps the robot balanced is the actuation of the wheels at the base of the robot (essentially an acceleration to arrest the falling motion). In order to make this happen it was essential to acquire a pair of DC motors and a motor driver. As it turned out, the specific motor driver that we acquired would had certain requirements that hadn’t been carefully considered before hand. This ended up presenting a challenge which caused delay in out project.

DC Gearbox Motor

The specific motor that was chosen for our project came with the recommendation of Professor Skovira. The DC motor selected had a power input range between 3 and 6 VDC. Adafruit measured the motors to spin at 200 RPM and deliver 0.6 Nm of torque at 6 V. In hindsight, this value was probably too low for our robot as this figure only translates to around 35 cm/s. We had selected the motors before constructing the framework, so we did not realize how fast we needed to recover from a falling motion.

DRV8833

To control our DC motors we had to get a motor driver. We ended up choosing the DRV8833 as it was the Adafruit’s recommended motor driver for the DC Gearbox Motor. The input parameters to the DRV8833 are shown in the following figure:


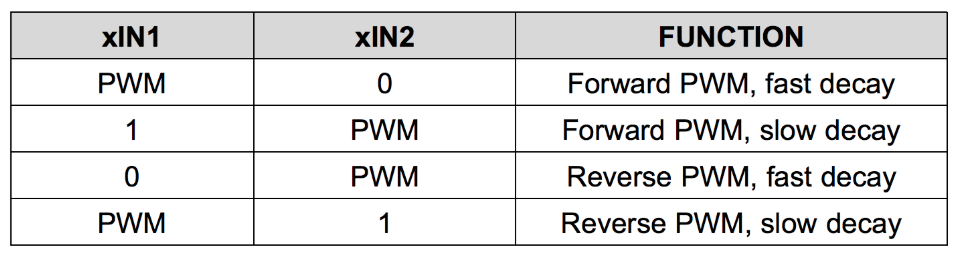
drv8833 input parameters
Image courtesy of adafruit.com

Inside the motor driver are two H-bridges that require two pins each (Ain1 and Ain2 or Bin1 and Bin2) to control the direction of one motor. One pin has to be high while the other has to be low for the motor to spin. Depending on which is high, the motor rotates in a certain direction. Since the robot has to quickly change its speed and direction to balance itself, a PWM signal is required at the “high” pin to control how fast the motor rotated while the low pin’s PWM signal temporarily has a duty cycle of 0.

Based on this input requirement, we needed four PWM signals for the two motors; two would have duty cycles of 0 and the other two would determine how fast the motors spun. However, after a while of testing and debugging, we realized that the Raspberry Pi only has 2 hardware PWM pins! This caused some initial panic as acquiring a new motor driver would take a while. Thankfully, with the help of Professor Skovira, a clever workaround was developed.

Transistor Network

With the help of Professor Skovira, we experimented with switching a PWM signal on and off using a transistor controlled by a GPIO pin. When the GPIO signal is “high”, the PWM signal is transmitted through to the input terminal of the motor driver. If the GPIO signal is “low” the PWM signal is cut off from the motor driver. Using this technique a single PWM signal could be split between two motor driver input terminals by having one active and one inactive transistor. This ended up reducing the number of required hardware PWM pins at the affordable price of four transistor controlling GPIO pins. The following is the final version of our transistor network:


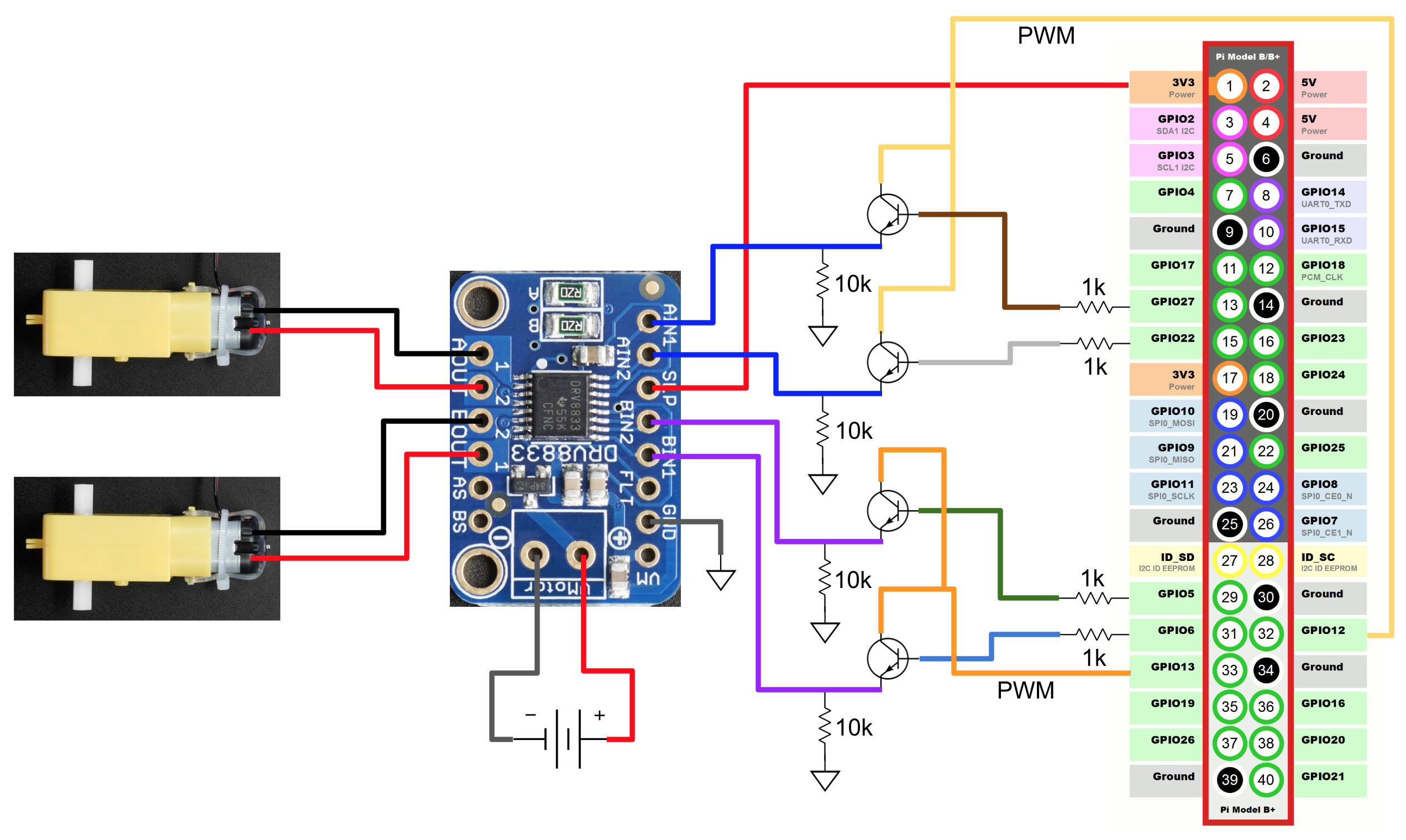
transistor network
Images courtesy of raspberrypi.spy.co.uk and adafruit.com

Control Algorithm

The vertical stance of the robot is an unstable equilibrium. Any small deviation from a perfectly vertical stance will cause the robot to swing away from that equilibrium due to the torque generated by gravity. Without any control mechanism in place, the robot will abruptly fall over on its side. To combat this, whenever the accelerometer/gyroscope sensor outputs an absolute orientation angle that deviates from this vertical, the control algorithm should speed up the motors in the direction that causes the wheels to be directly under the center of mass.

After much testing, a Proportional Derivative controller was found to be the most effective. The proportional component makes sure that error is minimized as quickly as possible, while the derivative control works to minimize overshoots past the most stable position that is caused by the proportional gain (effectively acting as a damping force). The proportional and derivative control terms vary based on the vertical angle offset, with the proportional term relating to the magnitude of the error and the derivative term depending on how fast the error is changing. Shown below are the equations (with change in time incorporated into kd):

Pterm = kp e

Dterm = - kd ( ei - ei-1 )

The highest duty cycle that corresponded to no wheel movement was easily determined to be about 62%. The sum of the two terms would be added to this duty cycle to increase the wheel speed, so with higher error, there will be a higher duty cycle. To delay the drifting further, we commanded one wheel to move faster than the other to make the robot turn. This way, there was less horizontal velocity and made it a bit easier to balance. The kp and kd constants were chosen experimentally and scaled so that they were large enough to be added onto the duty cycles. We tried adding an integral term, and tested extensively to tune it, but it always ended up doing worse than just the PD control.

Even after extensive tuning, we found our robot simply struggled to balance longer than 3 to 5 seconds. The robot would often have a couple seconds of small oscillations before they grew. At some point the oscillations would turn into a forward or backward drift. This drift would cause the robot to accumulate speed in a particular direction. The issue was that if the robot accumulated too much horizontal velocity, it would be unable to recover from a falling motion. This is because of the wheel speed saturation. To counter the drift problem, we tried to adjust the vertical offset angle thinking that it was the culprit behind the preferential drift. While this adjustment did indeed change the direction of the drift, it could never be fine-tuned so as to fully prevent the drift.

After hours of trial and error, it was further discovered that the direction of the robot and even the type of surface had some bearing on the drift problem. In a final effort to combat the drift, the balancing controls were updated to make the robot slowly spin. This was done by having the wheels turn at different rates. The idea behind this was that as the robot moves in circles the effects leading to drift would hopefully be cancelled out. While this approach didn’t get rid of the drift issue, it did manage to slightly increase the total balance time of the robot.

Result

Tuning the proportional and derivative terms proved to be more difficult than expected. There was a nonlinear relationship between velocity and PWM so corrections with PD control may not have been sufficient to provide the required amount of velocity change. In addition, the max motor torque of the wheel was too low. This resulted in the robot balancing while oscillating around the stable point at first, before the oscillations became too large and it entered the nonlinear regime. This was where the robot would just drift in one direction as the wheel speed was not fast enough to recover. Nevertheless, we managed to create a robot that balanced for a record of 10 seconds! It performed best when angles were small, the masking tape was placed at the right spot, and when the floor was the most even. We did not expect balancing to be this difficult, so our other objectives of sending radio commands and balancing objects were not realized (although we did prove that we could balance a masking tape!).

Conclusion

It is often said that controls tuning is much more of an art than it is a science. This has most definitely been the biggest takeaway from this project. The challenges and failures faced throughout this undertaking have greatly increased the respect that we have for other individuals who have successfully developed balancing robots. Nonetheless, as a first attempt we are happy and proud that we could at least make a robot that (under good circumstances) can balance for over 5 seconds before it begins to fall over. Without any control the same robot would topple over in a fraction of a second. Given more time we believe we would be able to crack down on many of the issues that were faced. In conclusion, in spite of the hardships and failures, we see that this undertaking has been an invaluable learning experience.

Future Work

There were many alternative design ideas that were largely unexplored due to the short duration of the project. These are in the areas of the robot structure, sensors, motors, and control algorithms. The following is an elaboration on what we would like to try in the future:

In terms of structure, we could have increased the width of our shelves, but placed the majority of the components such as the RPi and circuit boards on the top. This will make the robot significantly top-heavy and allow the motors to change faster. We could have also bought motors capable of higher voltage and RPM for obvious reasons.

For our control algorithm, a Linear Quadratic Regulator was considered to account for the nonlinear behavior of controlling the motors. It works by minimizing a cost function, which is our error in angle, but requires us to know several factors about our system exactly, such as moment of inertia, mass, and torque. The LQR also requires us to tune gains, but is much more exact than PID control, which may result in less oscillations for our robot. This alternative may have also allowed us to change the acceleration of our robot instead of the velocity, which is the main mechanism of balancing. Given our lack of experience in implementing this controller and our time constraints, we thought it best not to code this for our project. If given more time, we would have loved to explore this option.

The Team

Generic placeholder image

Alex and Jordan

Generic placeholder image

Alex Lui

al754@cornell.edu

Generic placeholder image

Jordan Brunson

jdb429@cornell.edu

Parts List

Total: ~ $85

References

LSM9DS1
BNO055
DRV8833
CircuitPython Library
LSM9DS1 Raspberry Pi Library
Pigpio Library
R-Pi GPIO Document

Acknowledgement

We sincerely thank Professor Skovira and the amazing lab TAs for their continuous help, guidance, and support. This course has been immensely enjoyable for the both of us.

Code Appendix


# Jordan Brunson (jdb429) & Alex Lui (al754)

import numpy as np
import RPi.GPIO as GPIO
import time
import pigpio
import sys
from busio import I2C
from board import SDA,SCL
import adafruit_bno055
import subprocess

print('Starting...')

# Setup calibration buttons
GPIO.setmode(GPIO.BCM)
GPIO.setup(23,GPIO.IN)
GPIO.setup(24,GPIO.IN)

# Setup BNO055 sensor
i2c = I2C(SCL, SDA)
sensor = adafruit_bno055.BNO055(i2c)

# Setup GPIO outputs
GPIO.setmode(GPIO.BCM)
GPIO.setup(5,GPIO.OUT)
GPIO.setup(6,GPIO.OUT)
GPIO.setup(22,GPIO.OUT)
GPIO.setup(27,GPIO.OUT)

# Setup hardware PWM
pi_hw = pigpio.pi()

# Set Parameters
duration = 600          # Sets the run time of the program
threshold = 0           # Sets the threshold angle
q = 80                  # Sets the length of the integral
z0 = -0.5               # Sets the zero angle offset

# Set PID gains
kp = 65000              # Proportional gain
ki = 10000              # Integral gain
kd = 250000             # Derivative gain

# Initialize Parameters
start = time.time()     # Start time
counter = 0             # Counting term
iterm = 0               # Integral term
button_wait = 0         # Wait button
t = time.time()         # Last recorded time
e = 0                   # Error term
e_prev = 0              # Previous error term
integral = np.zeros(q)  # Array of errors

try:
    print('Balance control active.')
    
    while(time.time() - start) < duration: 
        # Use buttons to change calibration zero during balance
        if button_wait == 0:
            if GPIO.input(23) == GPIO.HIGH:
                z0 = z0 - 0.0025

            if GPIO.input(24) == GPIO.HIGH:
                z0 = z0 + 0.0025

            button_wait = 20

        # Reset button_wait
        if button_wait != 0:
            button_wait = button_wait - 1
    
        # Count down timer
        if counter % 160 == 0:
            print (str(int(duration - (time.time() - start))))

        # Change calibrated zero angle based on average vertical angle deviation.
        # z0 = 1.625 - np.mean(integral)

        # Read euler angles
        x = sensor.euler[0]
        y = sensor.euler[1]
        z = sensor.euler[2]
    
        # Get error
        e = z-z0

        # Update array of errors
        integral[1:q-1] = integral[0:q-2]
        integral[0] = e

        # Compute PID terms
        pterm = kp*abs(e)
        iterm = ki*np.mean(integral)
        dterm = -kd*abs(abs(e) - abs(e_prev))*(1-abs(e)/4)

        # Compute outpt signal          
        output = int(pterm + dterm)

        # Store error in previous error term
        e_prev = e
    
        # Drift prevention: When the integrated average error is above
        # a certain threshold and the PWM velocity is already
        # considerably large, issue large PWM signal in the direction of
        # the drift so as to recover.
        if output > 200000 and abs(np.mean(integral)) > 0.5:
            output = 320000
    
        # Control maximum output so as to not exceed 100% duty cycle
        if output > 320000:
            output = 320000            

        # Set motor directions and speeds
        if e > 0 and abs(e) > threshold:
            GPIO.output(5,1)
            GPIO.output(22,1)
            GPIO.output(6,0)
            GPIO.output(27,0)
            pi_hw.hardware_PWM(12,50000,620000 + output)
            pi_hw.hardware_PWM(13,50000,680000 + output)
    
        elif e < 0 and abs(e) > threshold:
            GPIO.output(5,0)
            GPIO.output(22,0)
            GPIO.output(6,1)
            GPIO.output(27,1)
            pi_hw.hardware_PWM(12,50000,680000 + output)
            pi_hw.hardware_PWM(13,50000,620000 + output)
        
        else:
            pi_hw.hardware_PWM(12,0,0)
            pi_hw.hardware_PWM(13,0,0)

        # Update counter
        counter = counter + 1
    
finally:
    # Cleanup GPIO, turn off hardware PWM, and exit code
    pi_hw.hardware_PWM(12,0,0)
    pi_hw.hardware_PWM(13,0,0)
    GPIO.cleanup()
    print('Program shutdown.')